Любая особь популяции в процессе своей жизнедеятельности перемещается по ареалу — имеет свой радиус индивидуальной активности. Это понятие было впервые введено Н.В. Тимофеевым-Ресовским, а сам радиус может быть измерен экспериментально. Но об этом несколько позже. Заметим, что если этот радиус больше, чем характерный размер ареала, то популяцию можно считать хорошо перемешанной и при ее описании можно не учитывать пространственных эффектов. Если же мы имеем обратную картину, то рассмотрение пространственного распределения популяции становится просто необходимым.[ ...]
Что касается зависимости функции смертности D от плотности N, то практически для всех популяций D(N) — монотонно возрастающая функция, причем D(0) =т> 0, т — естественная смертность, а возрастание смертности с ростом iV объясняется ростом конкуренции за ограниченный ресурс (пища, пространство и т.п.).[ ...]
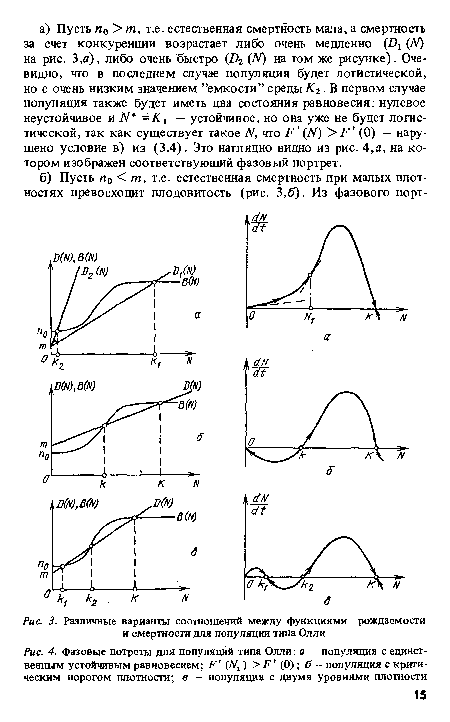
С функцией рождаемости В дело обстоит сложнее. Для многих видов она определяется лишь физиологическими пределами рождаемости и не зависит от N, так что В (N) = п = С(С — const), гдё п — это так называемая естественная рождаемость (или плодовитость) . Однако для многих видов животных, могущих мигрировать достаточно свободно и просторно заселяющих свой ареал, это предположение не совсем верно. Дело в том, что при малых плотностях размножение определяется, скорее,вероятностью встречи брачных партнеров, а не физиологической плодовитостью. Тогда зависимость В (N) будет иметь вид, изображенный на рис. 1. Популяции с таким типом зависимости В (JV) обычно называются популяциями типа Олли. Для них физиологический предел рождаемости достигается только при определенной плотности. Величина рождаемости при малой плотности (и0) обычно очень низка, но все-таки отлична от нуля.[ ...]
На рис. 2. изображен фазовый портрет обобщенной логистической популяции; очевидно, что она имеет два состояния равновесия :А7 = 0 — неустойчивое и Nf = К — устойчивое.[ ...]
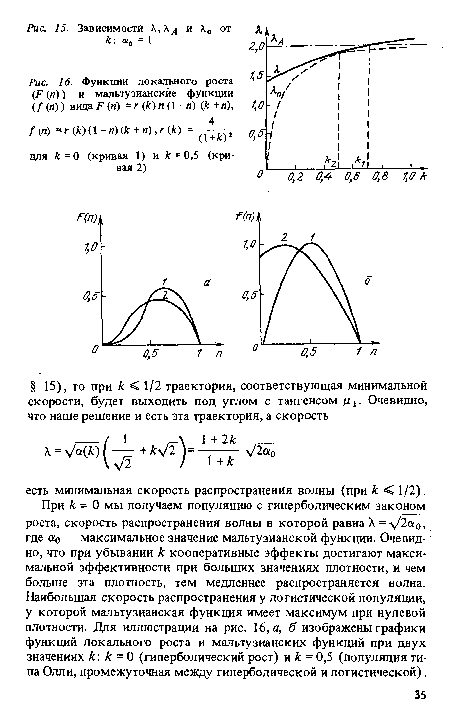
В предыдущем параграфе мы встречались с популяциями типа Олли и описывали их феноменологически. Но очевидно, что такая форма зависимости рождаемости от плотности есть следствие кооперативных взаимодействий особей в популяции.[ ...]
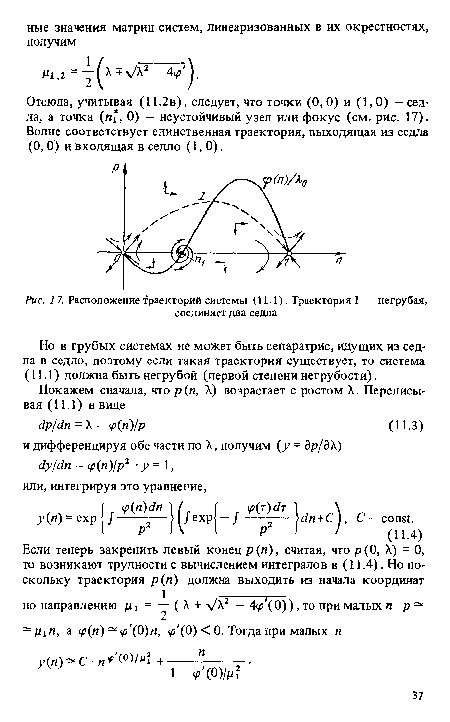
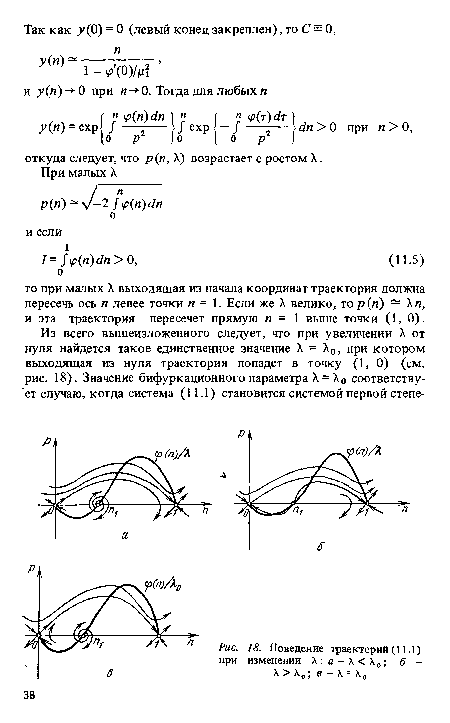
Из рис. 6 видно, что траектория р, не может пересечь ось IV, и следовательно, она вся лежит в положительном квадранте фазовой плоскости. Если теперь удастся доказать, что она не может пересечь ось р выше начала координат, то тем самым мы докажем, что она проходит через него.[ ...]
Рассмотрим луч р=СЫ (О 0) и покажем, что при подходящем выборе С ни одна траектория, начинающаяся в точке, лежащей на оси р и расположенной выше начала координат, не пересекает этот луч. Тем самым мы докажем, что ни одна такая траектория не может входить в точку (К, 0) по направлению 1.[ ...]
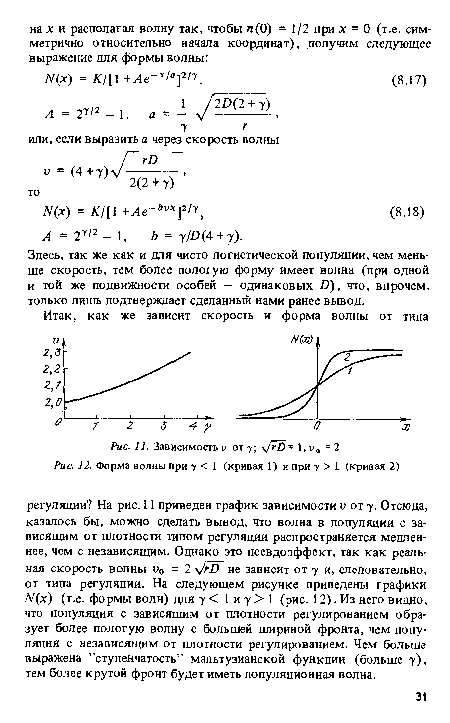
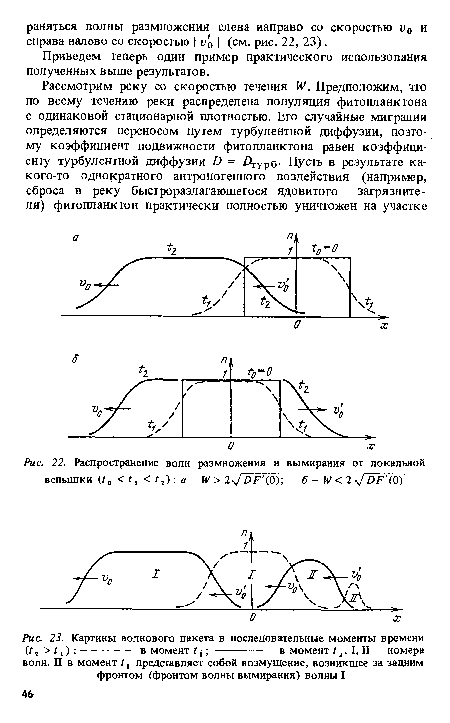
Мы получили непрерывный спектр возможных скоростей, ограниченный снизу величиной v0 =2 y/DF (0) . Возникает вопрос, какая из этих скоростей реализуется в действительности? Но прежде, чем переходить к рассмотрению этого вопроса, мы остановимся на одном любопытном эффекте, связанном с возможными типами волновых решений исходной задачи.[ ...]
Из (6.4) видно, что при t -> 00 v(t) стремится снизу к и0 = = 2 y/F (0)D - минимальной скорости распространения волны.[ ...]
Рисунки к данной главе:
Вернуться к оглавлению