Рис 9 6 Геометрическое распределение относительного обилия [140].[ ...]
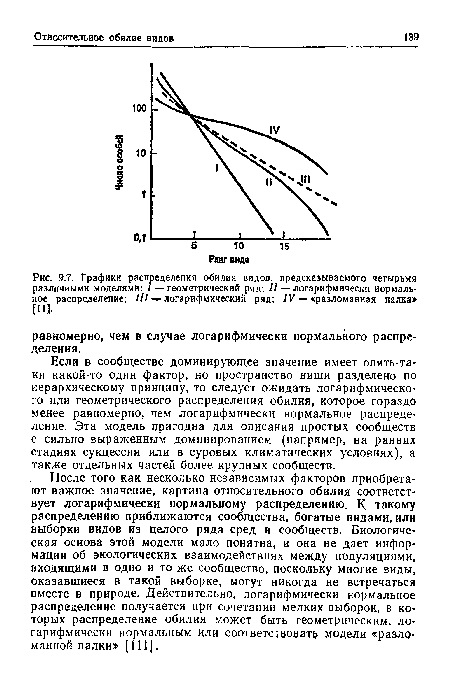
Эти различные модели образуют семейство взаимно пересекающихся кривых, в чем легко убедиться, если одновременно построить графики зависимости предсказываемых распределений логарифмов обилия от ранга видов (рис. 9.7). Когда динамика сообщества зависит главным образом от какого-либо одного фактора, пригодна модель «разломанной палки» как статистически реалистичное выражение равномерного распределения. Логарифмический ряд — это статистическое выражение неравномерного процесса, при котором возможен преимущественный захват ниш и идеальная форма которого описывается геометрической прогрессией [209]. Промежуточное положение между этими крайностями занимает логарифмически нормальное распределение, возникающее в среде, подверженной случайным, флуктуациям, и (или) когда в динамике обширной ассамблеи видов важную роль играют несколько факторов. Соответствие распределения обилия той или иной из этих моделей, по всей вероятности, выражает нечто существенное, касающееся данной группы видов. Вместо того чтобы выбирать модель, которая лучше всего описывает относительные обилия видов, следует выяснить, в каких случаях и почему они в данном сообществе приближаются к одному из рассмотренных распределений.[ ...]
Если в сообществе доминирующее значение имеет опять-та-ки какой-то один фактор, но пространство ниши разделено по иерархическому принципу, то следует ожидать логарифмического или геометрического распределения обилия, которое гораздо менее равномерно, чем логарифмически нормальное распределение. Эта модель пригодна для описания простых сообществ с сильно выраженным доминированием (например, на ранних стадиях сукцессии или в суровых климатических условиях), а также отдельных частей более крупных сообществ.[ ...]
После того как несколько независимых факторов приобретают важное значение, картина относительного обилия соответствует логарифмически нормальному распределению. К такому распределению приближаются сообщества, богатые видами, или выборки видов из целого ряда сред и сообществ. Биологическая основа этой модели мало понятна, и она не дает информации об экологических взаимодействиях между популяциями, входящими в одно и то же сообщество, поскольку многие виды, оказавшиеся в такой выборке, могут никогда не встречаться вместе в природе. Действительно, логарифмически нормальное распределение получается при сочетании мелких выборок, в которых распределение обилия может быть геометрическим, логарифмически нормальным или соответствовать модели «разломанной палки» 1П1].[ ...]
Геометрическое и логарифмически нормальное распределения могут на самом деле отражать крайности в величине выборки. Например, если объединить все данные по биомассе калифорнийских злаковых лугов, то получится логарифмически нормальное распределение. Если же постепенно выделять данные по отдельным травостоям, то распределение все больше и больше отклоняется от логарифмически нормального, приближаясь к геометрическому [6]. Подобным же образом в двух-выборках, взятых дночерпателем из соседних участков морского бентосного сообщества, обычно наблюдается совершенно различная картина доминирования, но если объединить пять или более выборок, то получится логарифмически нормальное распределение [257]. В небольших масштабах характер распределения сильнее зависит от биологических факторов, таких как хищничество, конкуренция, пополнение, дифференциальная смертность и т. п., поэтому, возможно, что геометрическое распределение описывает разделение пространства реализованных ииш между сосуществующими популяциями или в пределах отдельных гильдий. А логарифмически нормальное распределение, вероятно, описывает разделение пространства реализованных ниш между разными гильдиями или даже сообществами.[ ...]
Изменения в распределении видового обилия наблюдаются также в процессе сукцессии. Для ранних стадий сукцессии характерно геометрическое распределение, но в дальнейшем, по-видимому, на окончательный состав сообщества оказывает воздействие множество экологических факторов, что приводит к сдвигу в сторону логарифмически нормального распределения обилия (рис. 9.8). Это было показано для растительных сукцессий (хотя на поздних стадиях может произойти возврат к доминированию и геометрическому распределению [111] ) и для групп насекомых, в которых распределение обилия видов с течением сукцессии постепенно становилось более равномерным [264]. Этот сдвиг может быть прямым следствием возрастания неоднородности местообитания в соответствии с обсуждавшейся выше моделью равновесия сообщества [257]. Изменение этой картины на противоположную наблюдается при загрязнении зрелых сообществ [7], когда вновь становится необходимой адаптация к какому-то одному доминирующему фактору.[ ...]
Возникновение логарифмически нормального распределения при сочетании геометрических рядов свидетельствует о том, что лишь немногие виды обладают одновременно (а) широкой встречаемостью и высоким обилием или (б) ограниченной встречаемостью и низким обилием и что большинство видов (в) встречается со средним обилием в среднем числе сообществ, (г) достигает высокого обилия в небольшом числе сообществ или (д) встречается с низким обилием в большом числе сообществ [6].[ ...]
Изучение распределений относительного обилия все больше убеждает в том, что получаемые при этом графики можно лишь в ограниченной степени использовать для интерпретации взаимоотношений в сообществах и что это направление, вопреки возлагавшимся на него надеждам, не позволяет достаточно хорошо разобраться в структуре сообщества. Тем не менее рассмотренные здесь исследования пролили некоторый свет на зависимости между структурой и функциями сообщества, причем их результаты соответствуют данным, полученным при других подходах (см., например, гл. 3 и 6), а новые модели, разрабатываемые в направлении, начатом Сугихарой, по-видимому, позволяют надеяться на определенные успехи в будущем.[ ...]
Рисунки к данной главе:
| Графики распределения обилия видов, предсказываемого четырьмя различными моделями |
 |
![Распределение обилия видов в процессе сукцессии от залежи к сложному бору. Для исходного залежного сообщества (/) характерно геометрическое распределение. На более поздней стадии травяной растительности (2) распределение приближается к логарифмически нормальному На стадии (3) в ассамблею проникают древесные растения, которые постепенно становятся мощными доминантами (4), что ведет к понижению видового разнообразия. Кривая (5) отражает начало вторичного возрастания видового разнообразия [И].](/static/pngsmall/820485184.png)