Экология СПРАВОЧНИК

Для расчета влияния неровностей рельефа используется тот же самый метод, что и в случае невращающейся жидкости. Влияние вращения проявляется в изменении дисперсионных и поляризационных соотношений, которые уже рассматривались выше. В этом разделе мы сконцентрируем внимание на тех аспектах задачи, которые в сильной степени зависят от влияния вращения. Йри этом будем считать, что значение Ы]] велико, как это обычно имеет место в атмосфере и океане. Р авомфтри-ваемая жидкость предполагается несжимаемой и имеющей постоянную частоту плавучести N.[ ...]

Влияние вращения становится существенным, когда о> имеет порядок f, т. е. при горизонтальном масштабе порядка U/f. В атмосфере этот масштаб обычно в сотни раз превышает значение U/N, так что имеется значительный интервал волновых чисел, для которых U/N < A-1 <С U/f. В этом интервале справедливо гидростатическое приближение (поскольку горизонтальный масштаб велик по сравнению с вертикальным) и влияние вращения незначительно. Этот интервал будет называться областью гидростатики без вращения (см. разд. 8.4 и табл. 8.1). Масштаб U/ f , при котором влияние вращения играет заметную роль в поведении среды, обычно составляет в атмосфере 100 км и около 3 км для дна океана.[ ...]

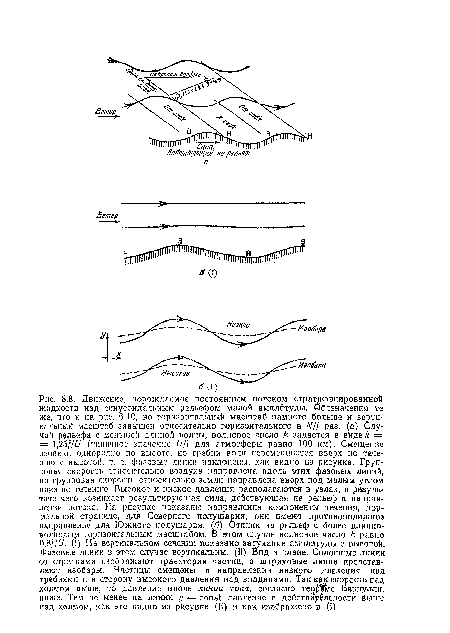
Зона высокого давления располагается с наветренной стороны, а низкого давления — с подветренной стороны, чем создается результирующая сила, действующая на возвышенность в направлении ветра. Результирующую силу сопротивления т, рассчитанную на единицу площади, можно вычислить следующим образом. Рассмотрим элемент увала с горизонтальными размерами 6х и б у и высотой б/г, как это изображено на рис. 8.6. Если бз есть ширина элемента, измеренная вдоль наклона, то сила, обусловленная давлением, имеет величину рбябг/ и направлена перпендикулярно к поверхности. Горизонтальная составляющая этой силы равна рбвбу, умноженной на б/г/б«, т. е.[ ...]

Давление р можно заменить его возмущением р (см. разд. 4.5.4), поскольку в невозмущенном состоянии не создает горизонтальную силу.[ ...]

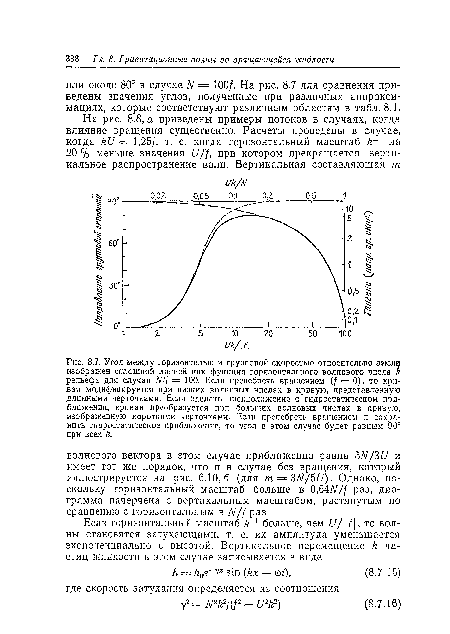
Как подчеркивалось в разд. 6.8 и будет далее показано в разд. 8.15, волны могут переносить горизонтальные напряжения, возникшие у земли, вверх до значительных высот, определяемых уровнями их поглощения. Скорость переноса обращается в нуль в двух крайних точках интервала существования волн при £-1 = и/N и /г 1 = и/ Ц. Однако когда к х в точности равно 17/ / , в решении возникает сингулярность. Это связано с тем, что если частота со = —1)к в точности равна инерционной, то имеет место резонанс. В этом случае из соотношения (8.7.6) видно, что т обращается в бесконечность (т. е. длина волны по вертикали очень мала) и возмущение скорости, определяемое формулой (8.7.7), также оказывается бесконечным. В действительности же большие значения т указывают на то, что трение стремится удалить эту компоненту волны и (или) важное значение приобретают нелинейные эффекты.[ ...]

Поперечное перемещение направлено над гребнями в сторону низкого давления, т. е. влево в Северном полушарии и вправо в Южном полушарии.[ ...]

Тот факт, что возмущение давления принимает высокие значения над гребнями увалов, где также высока скорость потока, на первый взгляд противоречит теореме Бернулли. Однако это противоречие кажущееся в силу того, что линии тока отклоняются в поперечном направлении больше, чем отклоняются изобары, в результате чего на линиях тока давление в действительности оказывается ниже именно над гребнями. Это можно увидеть на рис. 8.8,6, который демонстрирует специальный случай для Uk = 0,8/ с тем же самым увеличением N/f масштаба по вертикали и тем же самым продольным масштабом, как и на рис. 8.8, а. Нижняя часть рисунка изображает вид сверху. На нем можно заметить, что вдоль линии у = const давление над гребнями высокое, тогда как вдоль линий тока давление над гребнями низкое.[ ...]

Рисунки к данной главе:

Угол между горизонталью и групповой скоростью относительно земли изображен сплошной линией как функция горизонтального волнового числа й рельефа для случая ЫЦ = 100. Если пренебречь вращением (/ = 0), то кривая модифицируется при низких волновых числах в кривую, представленную длинными черточками. Если сделать предположение о гидростатическом приближении, кривая преобразуется при больших волновых числах в кривую, изображенную короткими черточками. Если пренебречь вращением и сохранить гидростатическое приближение, то угол в этом случае будет равным 90° при всех к

Движение, порождаемое постоянным потоком стратифицированной жидкости над синусоидальным рельефом малой амплитуды. Обозначения те же, что и на рис. 6.10, но горизонтальный масштаб намного больше ц вертикальный масштаб завышен относительно горизонтального в N/f раз. (а) Случай рельефа с меньшей длиной волны, волновое число k задается в вйде k = — l,25f/U (типичное значение U/f для атмосферы равно 100 км). Смещение изопикн однородно по высоте, но гребни волн перемещаются вверх по течению с высотой, т. е. фазовые линии наклонены, как видно из рисунка. Групповая скорость относительно воздуха направлена вдоль этих фазовых линий, но групповая скорость относительно земли направлена вверх под малым углом вниз по течению. Высокое и иизкое давления располагаются в узлах, в результате чего возникает результирующая сила, действующая на рельеф в направлении потока. На рисунке показаны направления компоненты течения, нормальной странице, для Северного полушария; они имеют противоположное направление для Южиого полушария, (б) Отклик на рельеф с более длйнио-вблйовым горизонтальным масштабом. В этом случае волновое число k равно 0,8¡IU. (1) На вертикальном сечении показано затухание амплитуды с высотой. Фазовые линии в этом случае вертикальны. (И) Вид в плане. Сплошные линии со стрелками изображают траектории частиц, а штриховые линии представляют изобары. Частицы смещены в направлении низкого давления над гребнями и в сторону высокого давления над впадинами. Так как скорость над холмом выше, то давление вдоль линии тока, согласно Teoflke Бернулли, нижа. Тем не менее на линии у «= const давление в д ейств й т&ль и о стй йыше над холмом, как это видно из рисунка (11) и как изображено в (1).

Вернуться к оглавлению