Экология СПРАВОЧНИК

Хотя полученное дисперсионное соотношение является точным, пользы от него в такой общей форме немного, так как в приложениях к океану или озерам глубина Н является настолько малой по сравнению с радиусом Россби (по меньшей мере в сотни раз), что с достаточной точностью вместо (8.2.1) можно использовать одно из предельных соотношений (либо при х 1 <а, либо при х 1 » ну По этой причине детальный вывод формулы (8.2.1) оставлен читателю в качестве упражнения, а мы перейдем к рассмотрению двух предельных соотношений.[ ...]

Прежде чем приступить к обсуждению свойств «поверхностных», или «баротропных» (см. разд. 6.2), волн, необходимо иметь в виду, что результаты изучения с одинаковым успехом можно приложить и к «внутренним», или «бароклинным», модам. Это следует из существования решений, полученных путем разделения переменных для уравнений стратифицированной жидкости в случае, когда горизонтальный масштаб велик по сравнению с вертикальным. Это свойство было показано в гл. 6. Таким образом, когда говорится о возвышении свободной поверхности или о компонентах горизонтальной скорости (и, v) для баротропного движения жидкости с глубиной Н, то те же рассуждения оказываются справедливыми и для внутренних течений, свойства которых могут быть Описаны в терминах эквивалентных переменных r (x,y,t), й(х,у, t) и v(x,y,t) теории мелкой воды и эквивалентной глубины Нв (см. разд. 6.11, 6.14 и 6.17).[ ...]

Эти уравнения имеют ненулевое решение только тогда, когда удовлетворяется дисперсионное соотношение (7.3.4), т. е.[ ...]

Для внутренних мод Я заменяется эквивалентной глубиной Я0. Если f равно нулю, то (8.2.9) дает соотношение между ускорением и градиентом давления, которое имеет место в предельном случае отсутствия вращения. Если оз равна нулю, то (8.2.9) эквивалентно геострофическому соотношению (7.2.14).[ ...]

Кроме того, уравнение потенциальной завихренности (7.2.8) показывает, что жидкость приобретает циклоническую завихренность при подъеме поверхности и антициклоническую завихренность, когда поверхность опускается, т. е.[ ...]

Тот факт, что возмущение потенциальной завихренности для волны Пуанкаре равно нулю, следует из (7.2.8) и предположения о виде зависимости от времени, пропорциональной ехр (—Ш).[ ...]

В океане энергия сосредоточивается в интервале низких частот. Это же характерно и для волны Пуанкаре, энергия которой концентрируется вблизи возможной наименьшей частоты таких воли, а именно инерционной частоты. Такие волны обнаруживают себя по близким к круговым ан-тициклоиическим орбитам и по частотам, близким к инерционной. Первый пример уверенного наблюдения такого движения был приведен в [282] и рассмотрен Дефантом [164, т. 1 с. 447].[ ...]

Наблюдения были произведены в Балтийском море (57,8° с.ш., 17,8° в. д., глубина 100 м). На рис.[ ...]

Тот факт, что траектории частиц не являются прямолинейными, как это происходит в невращающейся жидкости, имеет важные последствия. Как указал Кельвин [778], это означает, что граничное условие отсутствия нормального движения у плоской стенки не может быть удовлетворено за счет одиночной плоской бегущей волны. Возможные последствия этого обстоятельства будут исследованы в гл. 10.[ ...]

Рисунки к данной главе:

Волна Пуанкаре, бегущая слева направо, (а) Смещение свободной поверхности и (б) траектории частиц в плане, которые являются эллипсами с большими осями в направлении распространения волны (т. е. оси х) и малыми осями, равными //со, умноженной на длину больших осей. Частицы движутся по этим траекториям в антициклоническом направлении. Стрелки указывают положение частицы на свободной поверхности, а также направление движения для Северного полушария.

Результаты наблюдений течений и термальной структуры в верхнем 30 м слое озера Мичиган, август 3—5, 1963. Стрелки указывают направление и скорость, в соответствии с которыми образуется течение. Заштрихованная область указывает на слой термоклина, который заключен между 10 и 15° изотермами. Две диаграммы, которые перекрываются во времени, разделены интервалом в 17 ч., который является преобладающим периодом. Локальный инерционный период составляет 17,5 ч. Обратите внимание на примерно двухслойную структуру как в температуре, так и в скорости, и на аитициклоннче-ское вращение со временем векторов скорости.

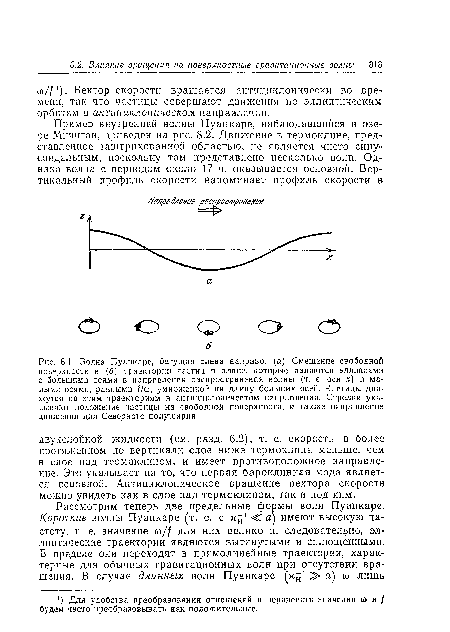
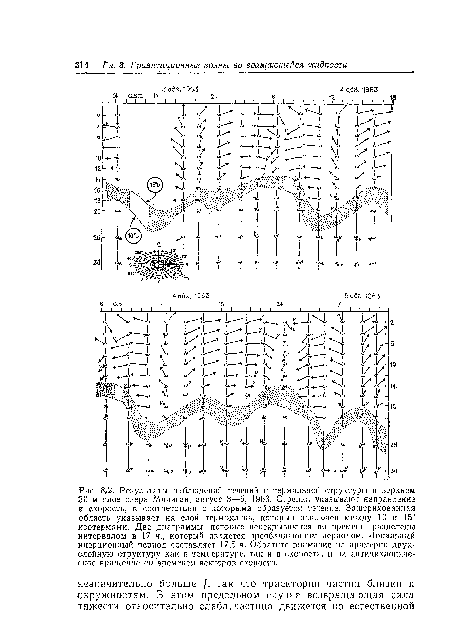
Исторические измерения течений в Балтийском море, осуществленные в [282], демонстрирующие колебания с периодом, близким к инерцнонпому. Нанесенная кривая представляет собой диаграмму поступательного вектора, показывающую то перемещение частицы, которое бы она имела при скорости, регистрируемой датчиком течения. Инерционный период составляет 14 ч. Указанные отметки разнесены на сутки. Обращает на себя внимание антициклоиическая направленность вращения.

Вернуться к оглавлению