Экология СПРАВОЧНИК

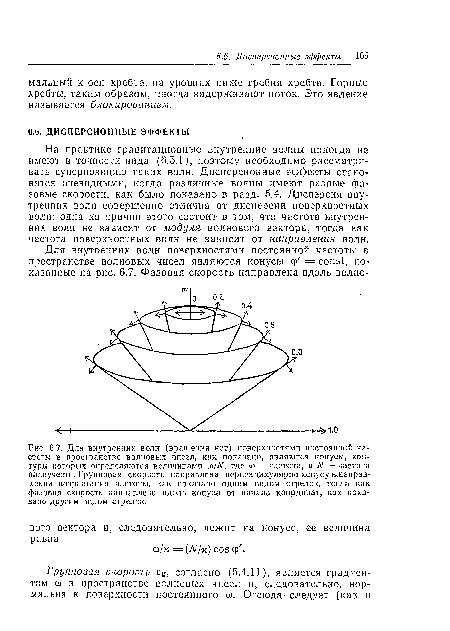
На практике гравитационные внутренние волны никогда не имеют в точности вида (6.5.1), поэтому необходимо рассматривать суперпозицию таких волн. Дисперсионные эффекты становятся очевидными, когда различные волны имеют разные фазовые скорости, как было показано в разд. 5.4. Дисперсия внутренних волн совершенно отлична от дисперсии поверхностных волн; одна из причин этого состоит в том, что частота внутренних воли не зависит от модуля волнового вектора, тогда как частота поверхностных волн не зависит от направления волн.[ ...]

Следовательно, модуль групповой скорости равен (A/ /x)sin ф , а ее направление составляет угол ф с вертикалью.[ ...]

Различие в направлениях фазового и группового распространения для внутренних волн хорошо иллюстрируется лабораторными экспериментами, в которых возмущения плотности можно сделать видимыми, используя шлирен-метод (метод полос) . В этом эксперименте, результаты которого показаны на рис. 6.9, энергия распространяется от колеблющегося цилиндра, рассматриваемого в первом приближении как точечный источник волн с фиксированной частотой со. Следовательно, энергия распространяется радиально в направлении распространения группы волн, т. е. она перемещается в пучках, угол <р которых с вертикалью задается соотношением (6.5.5). Видно, что линии постоянной фазы пересекают пучки трансверсально, и их движение направлено к горизонтальной плоскости, проходящей через источник. Эти и другие лабораторные эксперименты с внутренними волнами рассмотрены в [795].[ ...]

Таким образом, к увеличивается пропорционально времени, т. е. расстояние между волновыми гребнями уменьшается обратно пропорционально времени. Более подробное обсуждение решения для импульсного источника внутренних волн дано в 83], а дальнейшее обсуждение задачи в общем виде имеется в [854] и [456].[ ...]

Рисунки к данной главе:

Для внутренних волн (вращения нет) поверхностями постоянной частоты в пространстве волновых чисел, как показано, являются конусы, контуры которых определяются величинами a/N, где ш — частота, а N — частота плавучести. Групповая скорость направлена перпендикулярно конусу в-направ-лении возрастания частоты, как показано одним видом стрелок, тогда как фазовая скорость направлена вдоль конуса от начала координат, как показано другим видом стрелок.

Различие между дисперсионными характеристиками внутренних волн и поверхностных гравитационных волн, проиллюстрированное поведением соответствующей комбинации четырех прогрессивных волн, (а) Начальная конфигурация группы внутренних волн с волновыми гребнями, составляющими 60° с вертикалью. Показаны контуры возмущения давления, где оно равно максимальной величине, умноженной на 0,5. (б) Конфигурация спустя четыре периода. Группа сдвинулась параллельно гребням и вверх, в то время как отдельный гребень АА продвинулся на четыре длины волны вниз и влево. Чтобы сравнить это поведение с поведением поверхностных волн, предположим, что (а) теперь показывает вид диаграммы подобной комбинации поверхностных волн, контуры теперь будут там, где возвышение поверхности равно максимальному значению, умноженному на 0,5. Тогда (в) показывает конфигурацию спустя четыре периода. Волновой гребень АА снова сдвинулся на четыре длины волны, но теперь группа сдвинулась на две длины волны в том же направлении,

Полученные шлирен-методом картины внутренних волн, распространяющихся от цилиндра, который колеблется с частотой

Вернуться к оглавлению