Определение 1. Множество X из пространства Яп называется выпуклым, если из того, что две точки у и т. принадлежат этому множеству, вытекает, что и весь отрезок у, г = хе Я" : х = = Ху + (1 - Х)г, 0 < X < 1, соединяющий эти точки, также принадлежит этому множеству.[ ...]
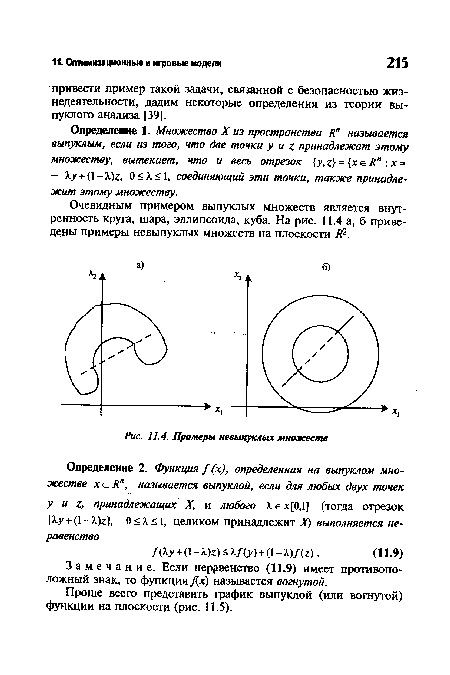
Очевидным примером выпуклых множеств является внутренность круга, шара, эллипсоида, куба. На рис. 11.4 а, б приведены примеры невыпуклых множеств на плоскости Я2.[ ...]
Замечание. Если неравенство (11.9) имеет противоположный знак, то функция /[х) называется вогнутой.[ ...]
Проще всего представить график выпуклой (или вогнутой) функции на плоскости (рис. 11.5).[ ...]
Правая часть неравенства (11.9) представляет собой отрезок АВ, соединяющий точки (у, f (у)) = А и В = (z,f (z)), причем каждая точка этого отрезка (на рисунке взята точка С) выше соответствующей точки графика (на рисунке точка £>). Если функция fix) достаточно гладкая, то условия выпуклости (вогнутости) можно выразить через ее вторую производную.[ ...]
В силу произвольности точки £, это неравенство справедливо на всем отрезке [у, z] и является условием выпуклости (в случае вогнутости справедливо обратное неравенство). Для иллюстрации рассмотрим два простых примера.[ ...]
Пример 1. /(х) = ех, х е (-оо,+<ю), /( ,) = ех > 0, следовательно, показательная функция выпукла на всей оси.[ ...]
Рисунки к данной главе:
| Примеры невыпуклых множеств |
 |
| График выпуклой функции на плоскости |
 |
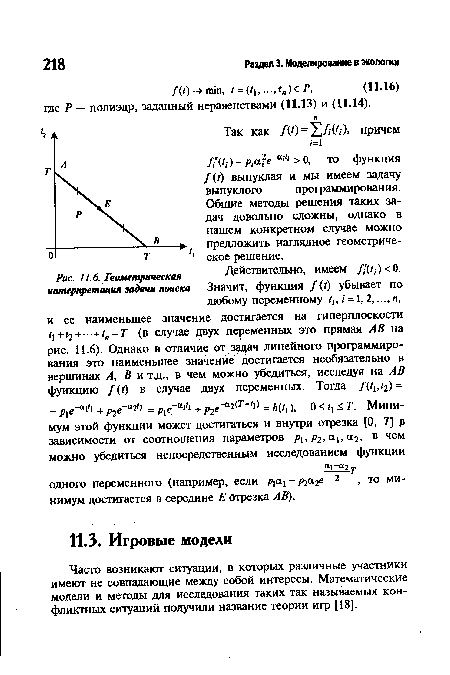
| Геометрическая интерпретация задачи поиска |
 |