Экология СПРАВОЧНИК

Задачу обтекания кругового цилиндра можно пытаться решить различными способами - аналитическими, численными или экспериментальными.[ ...]

Как всякое обтекание тел вязкой жидкостью, течение за цилиндром может быть описано системой уравнений Навъе-Стокса. Однако ввиду нелинейности уравнений и сложности задания граничных условий возникают принципиальные трудности получения теоретического решения. Поэтому первые попытки построения отрывного течения за цилиндром осуществлялись в рамках классической теории течений идеальной жидкости [Гельмгольц Г. Л. Ф., 1868; Кирхгоф Г. Р., 1869]. Однако такая математическая модель не давала удовлетворительного совпадения с опытными данными. Благодаря объяснению Л. Прандтля (1904) физической природы отрыва потока при больших числах Рейнольдса как отрыва пограничного слоя начался новый этап исследований обтекания тел с использованием асимптотических методов. Хотя эти методы дают приближенное решение задачи, однако они позволяют во многих случаях вскрывать физический механизм явления. В настоящее время наиболее значимые результаты дает метод построения сращиваемых асимптотических разложений [Сычев В.В. и др., 1987], основанный на использовании теории струй идеальной жидкости и теории пограничного слоя. В то же время полуэмпирический характер всех теоретических схем этого направления ограничивает их применение. Отметим, что в рамках почти каждой существующей полуэмпири-ческой теории решалась задача плоского обтекания кругового цилиндра [Девнин С.И., 1983; Сычев В.В. и др., 1987].[ ...]

Отметим, что в последние два десятилетия эффективным способом расчета течения за круговым цилиндром при больших числах Рейнольдса стал метод дискретных вихрей, основанный на модели идеальной жидкости и задании начальной интенсивности вихрей в точках отрыва потока (см., например, [Stansby Р.К., 1981; Белоцерков-ский С.М. и др., 1983]). Более подробная библиография применения метода дискретных вихрей в задаче плоского обтекания цилиндра приведена в работах [Ахмеров P.P. и др., 1987; Гоман О.Г. и др., 1993]. В то же время, для того чтобы получить этим методом необходимые данные о пульсациях скоростей и давлений на обтекаемой поверхности цилиндра, нужно знать характеристики среднего течения, обычно определяемые экспериментальным путем.[ ...]

В это же время информация о вихревых дорожках получалась в основном из фотографирования траекторий частиц. Состояние проблемы о вихревых дорожках на этот период времени приведено в обзорных работах [Krzywoblocki M.Z., 1953; Вилле Р., 1963].[ ...]

Рассмотрим современное представление о влиянии некоторых факторов на обтекание кругового цилиндра большого (бесконечного) удлинения. Заметим, что в экспериментальной аэродинамике практически достаточно большим удлинением общепринято считать расположение концов цилиндра от стенки до стенки рабочей части аэродинамической трубы либо когда на концах цилиндра установлены шайбы большого размера.[ ...]

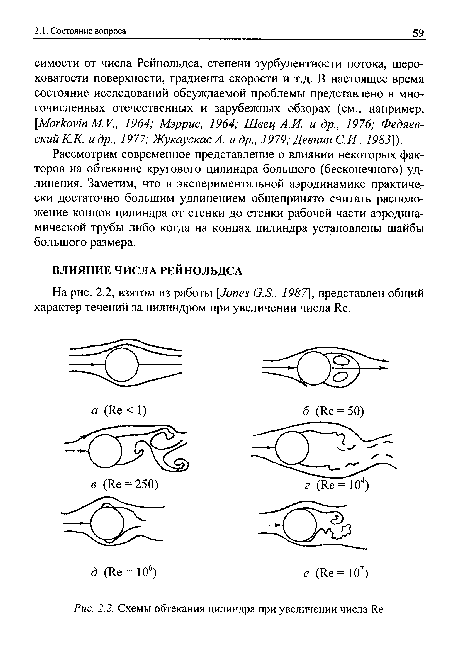
На рис. 2.2, взятом из работы [Jones G.S., 1987], представлен общий характер течений за цилиндром при увеличении числа Re.[ ...]

Отметим, что здесь изображены упрощенные схемы сложных картин течения. В отдельных случаях картины течений могут изменяться во времени или быть иными при промежуточных значениях чисел Яе, а при определенных условиях может наблюдаться трехмерное течение.[ ...]

В настоящее время считается общепризнанной введенная А. Рошко [КояИкоА., 1961] классификация режимов обтекания цилиндров. Согласно этой классификации различают четыре диапазона чисел Яе, переход между которыми сопровождается изменением характера обтекания цилиндра (рис. 2.2).[ ...]

Докритический режим обтекания (40 < Яе < 2-105) характеризуется ламинарным отрывом пограничного слоя (ф0Тр 82°). При этом свободные линии тока оторвавшегося течения выпуклы. В прилегающем к цилиндру потоке сдвиговые слои на некотором расстоянии от цилиндра свертываются в вихри, образуя вихревую дорожку с выделенной частотой, соответствующей числу 8Ь 0,2.[ ...]

Рисунки к данной главе:

Зависимость коэффициента лобового сопротивления цилиндра от числа Re (из работы [Jones G.S., 1987])

Схемы обтекания цилиндра при увеличении числа Re

Зависимость числа ЭЬ от числа Яе при поперечном обтекании кругового цилиндра бесконечного удлинения ([Эрикссон Л.Э., 1979])

Зависимость Сх =/(Яе) для кругового цилиндра, с указанием областей различных режимов (из работы [Эрикссон Л.Э., 1979])

Зависимость коэффициента сопротивления кругового цилиндра от числа Яе при различной степени турбулентности внешнего потока (из книги [Девнин С.И., 1983])

Схема обтекания консольного цилиндра пограничным слоем (из книги [Брэдшоу П., 1974])