Зная величину раздражений красных, зеленых и синих нервных центров, обусловленных каким-нибудь цветом, т. е. зная его цветовой тон, можно, пользуясь графическим методом, при помощи треугольника Ньютона, определить и насыщенность цвета.[ ...]
Цветовой тон может быть выражен, как было указано на стр. 34, величиной раздражения красных, зеленых и синих нервных центров.[ ...]
Ньютон предложил для графического изображения цветов пользоваться равносторонним треугольником, в вершинах которого находятся красный, зеленый и синий цвета (рис. 17). Положение всякого цвета на площади такого треугольника определяется совершенно определенной точкой, которая может быть найдена, если известны величины раздражения красных, зеленых и синих нервных центров.[ ...]
Положение цвета на площади треугольника находят, пользуясь аналогией с нахождением центра тяжести трех грузов, подвешенных в вершинах треугольника.[ ...]
При определении местоположения цвета на площади треугольника вместо грузов в расчет принимают определенные ка-ким-нибудь способом раздражения красных, зеленых и синих нервных центров. Предположим, что эти раздражения для какого-нибудь цвета равны: И = 0,5, й = 0,3 и В = 0,2.[ ...]
Применяя правило для нахождения центра тяжести, можно по величине раздражений нервных центров найти на площади треугольника положение цвета, вызывающего эти раздражения.[ ...]
Таким образом точка, определяющая цвет, вызывающий раздражение Я = 0,5, 0 = 0,3 и В — 0,2, поместится на площади треугольника в точке N. В этой точке расположится только один этот цвет. При малейшем изменении хотя бы одного раздражения точка, определяющая положение цвета на площади треугольника, переместится. И, наоборот, если известно положение точки на площади треугольника, то можно найти величины трех раздражений, которые определяют положение этой точки на площади.[ ...]
Так, например, зная положение точки N, проводим через нее и синюю вершину треугольника прямую. Определив по чертежу, что расстояние Л/Л/ в четыре раза меньше, чем расстояние от N до синей вершины, и разложив раздражение, равное 1, на величины, обратно пропорциональные этим расстояниям, мы найдем, что раздражение, соответствующее точке N, можно разложить на два, из которых одно раздражение, равное 0,2, приложено в синей вершине треугольника, а равное 0,8 — в точке М. Разложив таким же образом это раздражение, найдем /? = 0,5 и б = 0,3. Следовательно, положение точки N соответствует Я = 0,5, й = 0,3 и В = 0,2.[ ...]
Если все три раздражения, определяющие цвет, увеличить или уменьшить в одно и то же число раз, то, как легко убедиться, положение точки на плоскости треугольника не изменится, а так как одинаковое изменение всех трех раздражений вызывает только изменение яркости цвета, то очевидно, что цвета одного цветового тона и одинаковой насыщенности, различающиеся между собой только по яркости, поместятся в одной точке. Следовательно, каждому из цветов, между которыми существует качественное различие (по цветовому тону и насыщенности), соответствует своя точка на площади треугольника; цвета же, которые различаются только количественно (по яркости), помещаются в одной точке; поэтому определить яркость цвета по положению цветовой точки в треугольнике — нельзя.[ ...]
На стр. 34 приведены раздражения нервных центров, производимые светом различных длин волн. Пользуясь этими величинами, можно найти на площади треугольника ряд точек, из которых каждая соответствует одному из спектральных цветов.[ ...]
Рисунки к данной главе:
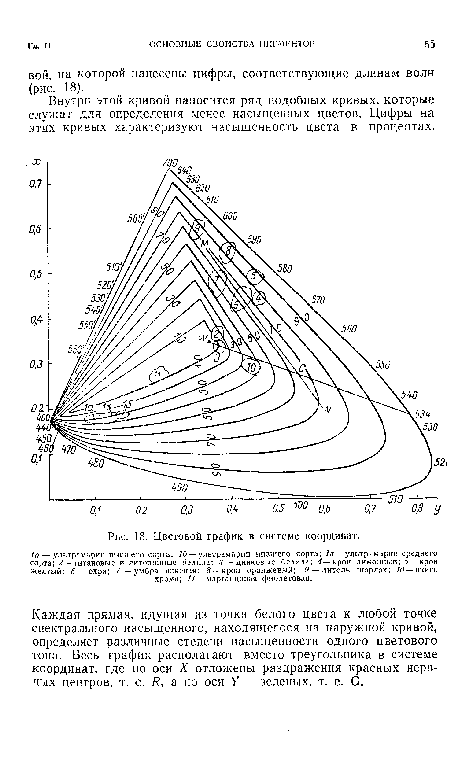
| Цветовой график в системе координат. |
 |