Предположим, что безразмерная величина ущерба (У) нелинейно зависит от физических масштабов (X) бедствия (расхода или уровня воды), например, пусть У = Хт(т > 1). Смысл этой зависимости заключается в том, что материальные и человеческие потери сильно увеличиваются, если только расход или уровень превысит некоторое характерное значение; в противном случае ущерб будет небольшим, т.е. небольшие превышения критического уровня расхода сопровождаются сильным нелинейным увеличением ущерба.[ ...]
Следовательно, распределение Парето возникает в результате суперпозиции двух нелинейных зависимостей - величины речного стока от влагозапасов бассейна и величины ущерба от физических характеристик наводнения.[ ...]
Таким образом, в соответствии со степенной статистикой катастрофические наводнения на нашей планете не являются экзотическими событиями.[ ...]
Исследования в этих направлениях уже проводятся по программе ЭКОС (изучение Земли как единой самоорганизующейся климатоэкологической системы), разработанной в Институте космических исследований РАН совместно с другими институтами [Космические исследования..., 1995]. Особое внимание эта программа уделяет изучению взаимодействия различных природных сред (атмосферы, гидросферы, криосферы, биосферы) при помощи средств дистанционного зондирования с целью выявления основных закономерностей функционирования Земли как единой экологической системы, подверженной воздействию антропогенных и природных факторов.[ ...]
Рисунки к данной главе:
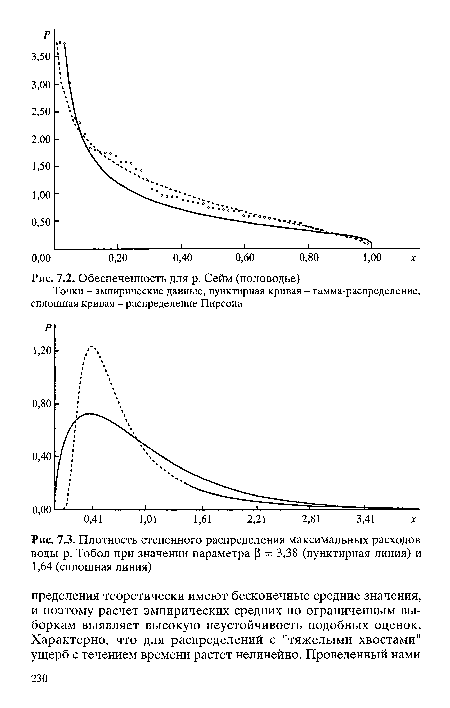
| Плотность степенного распределения максимальных расходов воды р. Тобол при значении параметра Р = 3,38 (пунктирная линия) и 1,64 (сплошная линия) |
 |
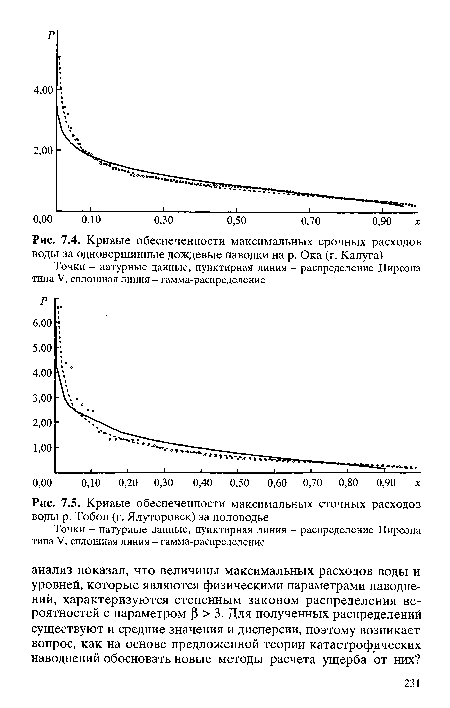
| Кривые обеспеченности максимальных сточных расходов воды р. Тобол (г. Ялуторовск) за половодье |
 |
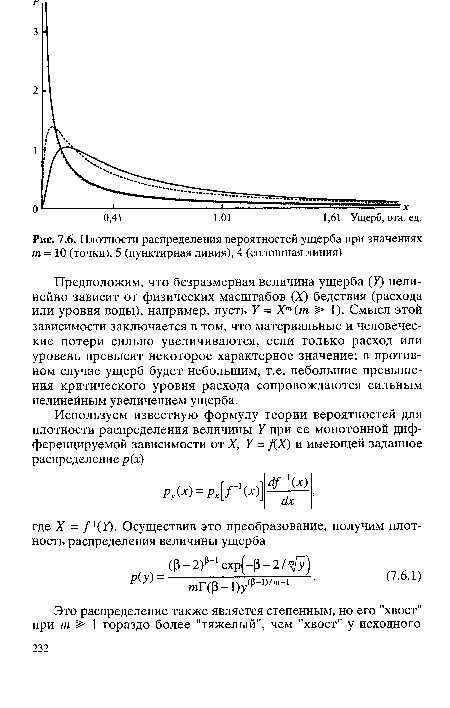
| Плотности распределения вероятностей ущерба при значениях т = 10 (точки), 5 (пунктирная линия), 4 (сплошная линия) |
 |