Взвешенные в воде мельчайшие частицы находятся в беспорядочном движении. Это явление систематически исследовал Р. Броун в 1827 г., и в его честь оно получило название броуновского движения. Причина такого движения долго оставалась загадкой. Удовлетворительное объяснение отсутствовало вплоть до 1905 г., когда А. Эйнштейн опубликовал свое объяснение. Практически именно объяснение броуновского движения, данное Эйнштейном, нужно считать началом стохастического моделирования природных явлений. Первое математически четкое построение теории броуновского движения было дано Н. Винером в 1918 г. С этого момента у броуновского движения появился синоним - винеровский процесс.[ ...]
А.Н. Колмогоров в 1940 г. впервые рассмотрел процессы, для которых DXt = t2H, i O, 0= Я 1,и назвал их спиралями Винера [Колмогоров, 1940]. Так появилось обобщение винеровского процесса, которое впоследствии развивалось Б. Мандельбротом [Mandelbrot,van Ness, 1968].[ ...]
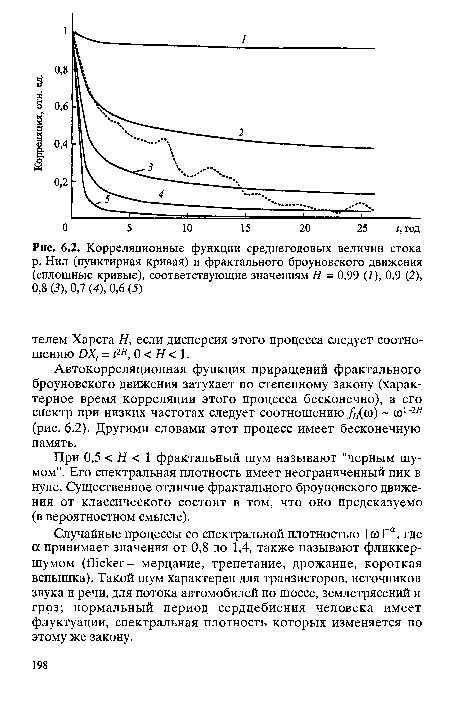
Автокорреляционная функция приращений фрактального броуновского движения затухает по степенному закону (характерное время корреляции этого процесса бесконечно), а его спектр при низких частотах следует соотношению fH(со) со 2я (рис. 6.2). Другими словами этот процесс имеет бесконечную память.[ ...]
При 0,5 < Я < 1 фрактальный шум называют "черным шумом". Его спектральная плотность имеет неограниченный пик в нуле. Существенное отличие фрактального броуновского движения от классического состоит в том, что оно предсказуемо (в вероятностном смысле).[ ...]
Случайные процессы со спектральной плотностью I со Г“, где а принимает значения от 0,8 до 1,4, также называют фликкер-шумом (flicker- мерцание, трепетание, дрожание, короткая вспышка). Такой шум характерен для транзисторов, источников звука и речи, для потока автомобилей по шоссе, землетрясений и гроз; нормальный период сердцебиения человека имеет флуктуации, спектральная плотность которых изменяется по этому же закону.[ ...]
Явление фликкер-шума исключительно широко представлено в природе. Оно характерно практически для всех сложных систем, как естественного, так и искусственного происхождения, и его примеры можно найти в самых разных областях - от биологии до астрофизики. Такое поведение спектра мощности на низких частотах означает, что значительная часть энергии связана с очень медленными процессами. Пользуясь метеорологической аналогией, можно сказать, что в таких системах нельзя предсказывать погоду, отвлекаясь от изменения климата. Сколько бы мы не накапливали информации о поведении системы, всегда найдутся важные процессы, которые начинают сказываться на временах, соизмеримых со временем изучения системы, т.е. те процессы, которые еще не успели проявиться, но которые непременно преподнесут нам неприятные сюрпризы (классический пример - поведение уровня Каспийского моря). Наличие в системе фликкер-шума означает возможность больших флуктуаций (наводнения, засухи, внезапные повышения или понижения уровня воды в водоемах), т.е. внутренне присущую гидрологической системе склонность к катастрофам.[ ...]
Если использовать для моделирования расходов Нила процесс фрактального броуновского движения, то соответствующий показатель Харста равен 0,7. Таким образом, эффект Харста получает математическую интерпретацию: колебания стока Нила - случайный процесс с бесконечной памятью. Однако эта аппроксимация является формальной, так как нет ответа на главный вопрос: какими законами физики обусловлен эффект Харста.[ ...]
Рисунки к данной главе:
Вернуться к оглавлению