Параметры X и р отражают силу указанных зависимостей. Значения X в основном зависят от климатических параметров (радиационного баланса, скорости ветра, влажности и температуры воздуха), а также от теплофизических свойств почвогрунтов бассейна. Песчаник, суглинок, песчаная степь, торфяники имеют различную пористость, их коэффициенты тепло-, влаго- и температуропроводности сильно различаются. Параметр (3 существенно зависит от вязкости воды, пористости почвогрунтов, наличия трещино-карстовых отложений и т.д.[ ...]
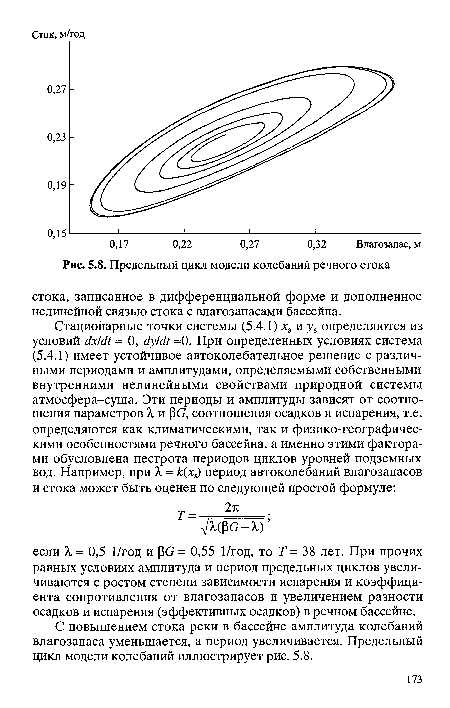
С повышением стока реки в бассейне амплитуда колебаний влагозапаса уменьшается, а период увеличивается. Предельный цикл модели колебаний иллюстрирует рис. 5.8.[ ...]
Наиболее яркую модель предельного цикла предложили лауреат Нобелевской премии М. Эйген и П. Шустер. "Представим, что с гор и горных плато вниз, в долину стекают ручьи и потоки, наполняя высокогорное озеро. Каждый ручей, каждый поток течет по своей траектории, которая зависит от гравитационного поля и особенностей ландшафта, а конечная точка всех траекторий предопределена. Но можно мысленно изменить гравитационное поле так, что все траектории, не достигнув озера, сольются в один поток, циркулирующий над долиной по некоторой замкнутой кривой. Это и есть предельный цикл по Эйгену" [Мучник, 1985].[ ...]
Механизм возникновения автоколебаний влагозапасов и речного стока можно рассматривать и с иных позиций. В самом деле, у нас есть неустойчивая точка, нелинейность процесса испарения, потенциально стабилизирующий элемент системы -речной сток - запаздывает по времени, так как расстояние между местом выпадения осадков и руслом реки велико (время добегания может составлять годы), поэтому здесь возможны автоколебания, подобные автоколебаниям в системах с запаздыванием. Например, натурные исследования [Соколов, Завилей-ский, Морунич, 1994] изотопными методами показали, что речные воды представляют смесь из разновозрастных, преимущественно подземных вод, причем для 50% вод характерен "возраст" 10-12 лет (даже для маленьких водосборов). Это означает, что математически описывать данное явление необходимо с помощью нелинейных дифференциальных (или дискретных) уравнений с запаздывающим аргументом .[ ...]
Можно представить и такую ситуацию. Допустим, что несколько водосборов генерируют колебания близкой частоты, тогда некоторый водосбор, генерирующий колебания другой частоты, может настроиться на колебания этих нескольких водосборов (за счет атмосферного переноса тепла и влаги), подобно тому, как смычковые и духовые инструменты, являясь автоколебательными системами, подстраиваются под некоторый средний фон всего оркестра (явление затягивания частоты). Именно этим механизмом автор данной монографии объясняет засухи, поражающие обширные территории. Физический механизм этого явления следующий. Допустим, что вследствие атмосферных процессов в течение ряда лет осадки малы. В этом случае влагозапас деятельного слоя суши резко падает, его прогреваемость ввиду уменьшения эффективной теплоемкости сильно увеличивается, что способствует еще большей диффузии влаги в атмосферу. Может возникнуть такая ситуация, что раскаленная поверхность суши будет превращать выпадающие осадки в пар еще в атмосфере, т.е. реакция суши на выпадение малого количества осадков будет существенно нелинейной. Адвективный перенос тепла и влаги в атмосфере будет распространяться и на соседние территории, осуществляя взаимодействие между речными бассейнами.[ ...]
Именно описанными выше автоколебательными режимами можно объяснить возникновение 200-летних периодов миграции и вторжений азиатских кочевников в 300-1600-е годы на северные территории, отмеченные в работе [Гончаров, 1994], а не долгопериодическим колебанием солнечной активности (см.[ ...]
Этим же механизмом может быть обусловлена и цикличность колебаний прироста годичных колец деревьев, загадочность возникновения которой давно волнует дендрологов. Со времени формирования первых приближенных представлений о взаимосвязи между факторами среды и приростом деревьев до наших дней выполнено множество оригинальных исследований, но по-прежнему вопрос о влиянии различных факторов на величину годичного прироста деревьев является одним из наиболее дискуссионных в экологической анатомии, физиологии, лесоведении и других научных дисциплинах, в которых годичные кольца деревьев используют в качестве индикаторов.[ ...]
На закономерную повторяемость прироста широких и узких колец обратил внимание еще Ф. Шведов (1892 г.), которому удалось построить на этой основе прогноз засух на территории черноземной полосы России. Несколько позднее американский астроном А. Дуглас (1919 г.), основываясь на результатах ден-дрохронологических исследований, разработал теорию климатических циклов. Отметим, что имеются в виду циклы различной продолжительности, а не только периоды колебаний чисел Вольфа (циклы в 11 и 22 года буквально заполонили геофизические исследования).[ ...]
В исследованиях Н.В. Ловелиуса построена принципиальная схема изменчивости прироста хвойных деревьев. Анализ обобщенного графика временной зависимости хода роста деревьев показал, что он имеет волновой характер. Закономерно повторяющиеся максимумы и минимумы внутривекового ритма проявляются на фоне восходящей волны ритма значительно большей продолжительности.[ ...]
Таким образом, учет взаимного влияния климатических и гидрологических процессов показал, что изменения средних значений запасов влаги, речного стока, испарения, амплитуды температурных колебаний поверхности суши за многолетний период времени имеют автоколебательный характер. Этот факт противоречит существующим постулатам стохастической гидрологии. Описание многолетних колебаний речного стока, уровней водоемов простыми цепями Маркова (или их усложненными модификациями), т.е. линейными уравнениями, неудовлетворительно с физической точки зрения, так как их решения единственны и глобально устойчивы. С учетом термодинамики необратимых процессов это означает, что гидрологическая система во всем диапазоне изменения своих параметров (температуры, скорости и влажности воздушных масс и т.д.) находится на термодинамической ветви и никогда не теряет устойчивость. Это очень смелое предположение, так как большинство реальных физических систем при достаточном удалении от состояния термодинамического равновесия ведут себя сложным образом. Но никаких оснований предполагать, что неустойчивости с существенно нелинейными эффектами, свойственные движению воздушных масс, движению воды в речном бассейне, процессам кристаллизации, конденсации и испарения воды, при усреднении исчезают, и гидрологическая система все время находится в устойчивом состоянии.[ ...]
Рисунки к данной главе:
| Предельный цикл модели колебаний речного стока |
 |