Если коэффициенты Ъц постоянны, а коэффициеты щ-линейные функции координат, то соответствующее уравнение Фоккера-Планка-Колмогорова имеет точное решение.[ ...]
Отметим, что при ц4 —» оо (время инерции стока очень мало) г—> 1, т.е. в этом случае речной сток функционально зависит от влагозапасов бассейна; на эту величину также влияют климатические факторы (испарение) и гидрогеологические особенности строения бассейна (коэффициент сопротивления).[ ...]
Уравнение (5.3.1) описывает колебания маятника под действием случайной силы.[ ...]
График автокорреляционной функции при различных значениях параметра к приведен на рис. 5.1.[ ...]
Зависимость спектральной функции от частоты приведена на рис. 5.2.[ ...]
Характерные периоды колебаний приращений стока некоторых рек, полученные методом моделирования на основе спектрального анализа временных рядов натурных данных, приведены в табл. 5.1.[ ...]
Для стационарного случайного процесса, описываемого уравнением (5.3.1), задача о выбросах решена полностью, т.е. определены вероятности заданного числа выбросов в течение данного промежутка времени и установлен закон распределения времени пребывания случайных процессов выше заданного уровня.[ ...]
Рисунки к данной главе:
| Автокорреляционная функция речного стока при Н = 0,2 (/), 0,1 (2), 0,5 (5) и п = 1,28 |
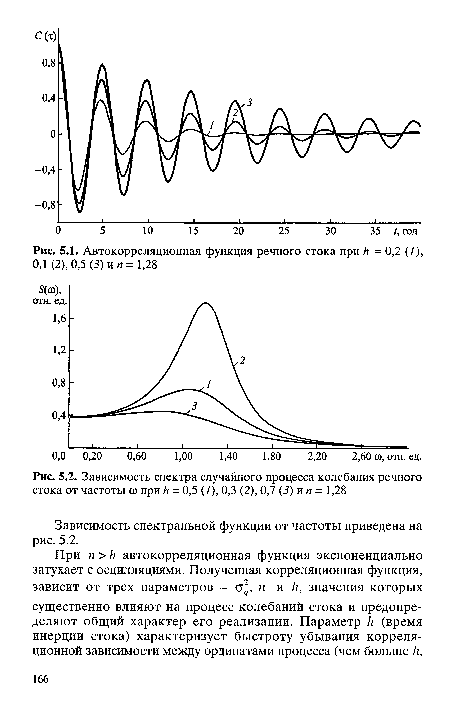 |
| Зависимость спектра случайного процесса колебания речного стока от частоты со при Н = 0,5 (7), 0,3 (2), 0,7 (3) и п = 1,28 |
 |
| Зависимость спектральной функции от частоты со для временных рядов приращений стока сибирских (а) и американских (б) рек |
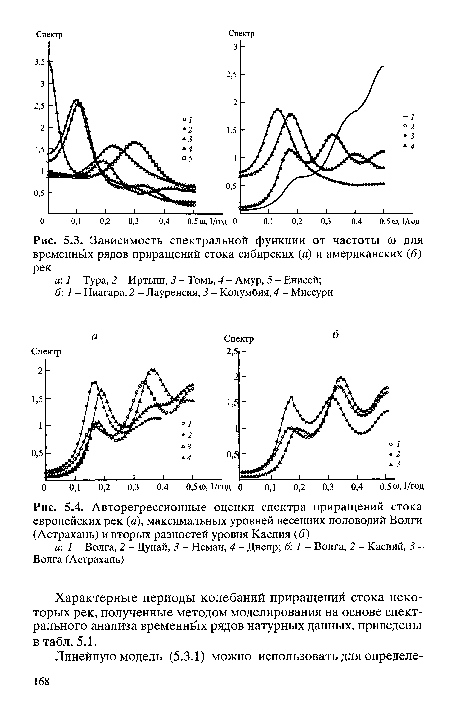 |
| Авторегрессионные оценки спектра приращений стока европейских рек (а), максимальных уровней весенних половодий Волги (Астрахань) и вторых разностей уровня Каспия (б) |
 |
| Зависимость числа выбросов стока р. Волги от уровня водности |
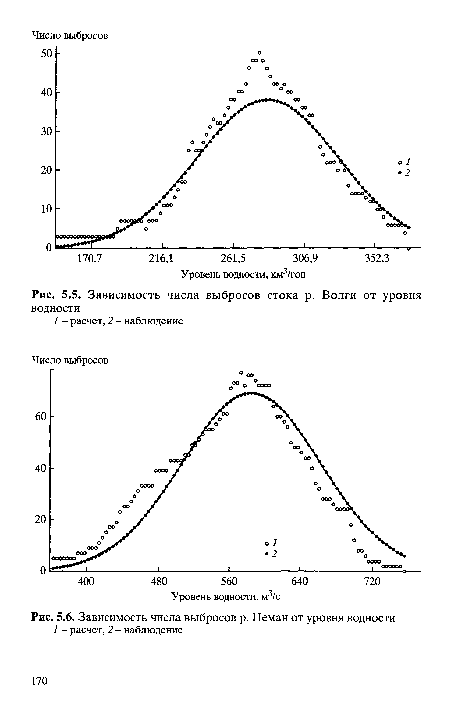 |
| Зависимость числа выбросов р. Неман от уровня водности 1 - расчет, 2 - наблюдение |
 |
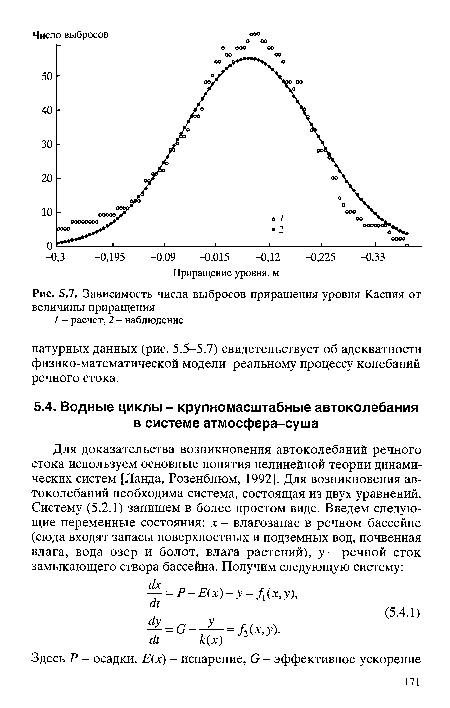
| Зависимость числа выбросов приращения уровня Каспия от величины приращения |
 |