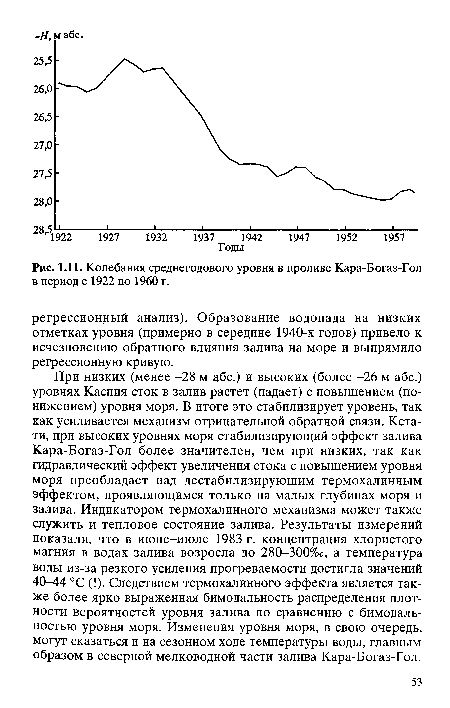
Механизм тепловой неустойчивости процесса испарения мелководных участков Каспийского моря может проявиться в дестабилизирующем влиянии залива Кара-Богаз-Гол (до отсоединения его дамбой 1980 г.) на уровенный режим моря. При этом важна не только малая глубина, а следовательно, и хорошая прогреваемость, но и высокая степень минерализации вод залива. Если до момента катастрофического падения уровня моря (1830-1939 гг.) соленость рассолов залива составляла 180%с, то уже к 1940 г. концентрация солей увеличилась до 300%с и в заливе началась кристаллизация поваренной соли. Уровень воды в заливе стремительно понижался, существенно опережая падение уровня Каспийского моря: если в 1921 г. разность этих уровней составляла 44 см, то в 1947 г. - 3,17 м, а в 1955 г. - 3,8 м.[ ...]
Известно (см. снимки из космоса 3.4, 3.5, на стр. 90-91 в работе [Кара-Богаз-Гол. Вчера, сегодня, завтра, 1988]), что усыхание залива происходило в 5(!)раз быстрее по сравнению с прогнозными оценками.[ ...]
Математически термохалинный механизм неустойчивости залива можно проиллюстрировать следующим образом.[ ...]
Рассмотрим проблему устойчивости водного баланса Каспийского моря в соответствии со схемой исследования задач устойчивости по Ляпунову.[ ...]
Здесь Нх,Н2,5х,52 - уровни моря и залива и их площади соответственно, <2 - речной приток, д - сток морской воды в залив, £2- слои видимого испарения (физический слой испарения минус осадки) с поверхности моря и залива.[ ...]
Сток морской воды в залив можно интерпретировать как подтопленный водослив с широким порогом, поэтому по законам гидравлики величина слоя стока в залив Кара-Богаз-Гол является функцией уровня моря и разности уровней моря и залива, т.е. д = д(Н1,Н1-Н2).[ ...]
Это состояние равновесия соответствует особой точке - узлу.[ ...]
Процесс отделения залива Кара-Богаз-Гол от Каспийского моря неоднократно происходил в прошлом, о чем свидетельствуют исследования отложений солей.[ ...]
Наличие этой неустойчивости радикально меняет весь механизм колебаний уровня Каспийского моря, для описания которого необходим подход с позиции теории сложных систем. В этом случае динамическая система уравнений водного баланса оказывается существенно нелинейной, характер ее решений меняется: возникают не единственные и неустойчивые решения -необходимые атрибуты ее сложной эволюции. При учете случайных вариаций параметров системы (например, количества осадков и речного стока) решения стохастических дифференциальных уравнений имеют бимодальное распределение и "вездесущность гауссовского распределения" уже теряет свою силу. Для анализа такого рода процессов необходим принципиально новый подход: линейные стохастические модели, которые так популярны в гидрологии, здесь малопригодны.[ ...]
Рисунки к данной главе:
| Колебания среднегодового уровня в проливе Кара-Богаз-Гол в период с 1922 по 1960 г. |
 |