Построение оптической модели разорванной облачности, учитывающей все многообразие и сильную изменчивость факторов, определяющих оптические и, следовательно, радиационные свойства облаков, является трудноразрешимой задачей. Рассматриваемые здесь математические модели облачных полей представляют собой упрощение действительности. Справедливость радиационной модели разорванной облачности определяется ее способностью адекватно описывать данные натурных измерений. К сожалению, экспериментальные исследования статистических характеристик полей облачности и радиации не являются комплексными, одновременно не ойределяются основные оптико-геометрические параметры облаков, альбедо подстилающей поверхности, зенитный угол Солнца и т. д. Это обстоятельство является серьезным препятствием корректного количественного сравнения теории с экспериментом.[ ...]
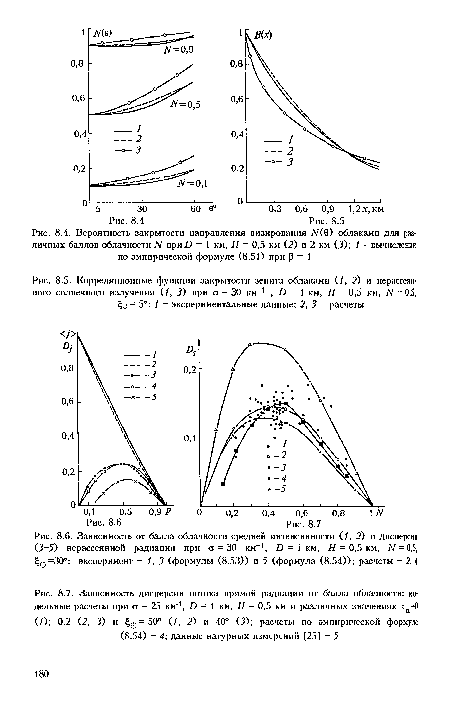
При Я = 0,5 км теоретические и экспериментальные характеристики закрытости направлений визирования кучевыми облаками хорошо согласуются (рис. 8.4 и 8.5), поэтому в дальнейших расчетах используется это значение Н. Функция Ж0) вычислена только до значений 0 = 60°, поскольку при больших углах наблюдения плоскопараллельная модель дает большие ошибки, связанные с не-учетом сферичности реальной атмосферы.[ ...]
Влияние молекулярно-аэрозольной компоненты на дисперсию прямой радиации иллюстрирует рис. 8.7, где также представлены расчеты по формуле (8.95) и экспериментальные данные [25]. В эксперименте не приведены даже грубые оценки пределов изменения зенитного угла Солнца, зависимости оптико-геометрических параметров облачного поля и оптической толщины от балла облачности, что не позволяет сделать однозначный вывод по результатам сравнения между полевыми измерениями и расчетами. Тем не менее, изменяя в разумных пределах %а и £0, можно получить удовлетворительное количественное и качественное согласие между теорией и экспериментом.[ ...]
При оценке величины Dg учитывалось ослабление подоблачной атмосферой только прямой радиации. При расчете статистики рассеянной радиации считается, что приемник расположен на нижней границе облачного слоя, поэтому не учитывается уменьшение в среднем амплитуды флуктуаций потока рассеянного света, которое наблюдается при увеличении расстояния от приемников до облаков. При малых и средних значениях N основной вклад в Dq вносит Ds [21], поэтому в данной области N сделанные выше предположения не приводят к существенным ошибкам в определении Dq.[ ...]
Удовлетворительное совпадение с экспериментом означает, что теория достаточно хорошо описывает не тольк© средние потоки, но и среднюю интенсивность солнечной радиации при кучевой облачности.[ ...]
Например, во всех имеющихся в настоящее время эмпирических формулах в явном виде не учитывается зависимость статистических характеристик лучистых потоков от таких важных параметров, как оптическая толщина и микроструктура облаков, альбедо подстилающей поверхности, а иногда и от зенитного угла Солнца. Теория же позволяет все это достаточно корректно учесть и исследовать из-меичнвость статистических характеристик излучения при вариациях оптических и геометрических параметров облачности, альбедо подстилающей поверхности, региональных, сезонных п дневных условии освещения.[ ...]
Сравнение результатов расчетов с данными натурных измерений показывает, что между теорией и экспериментом существует удовлетворительное согласие. Особо следует отметить, что эта согласованность не достигалась путем специального подбора параметров задачи, поэтому она не является результатом подгонки решения под известный ответ п позволяет считать, что пуассоновские модели облачных полей со случайной геометрией и уравнения для моментов интенсивности солнечной радиации в главных чертах правильно отражают реальный процесс формирования радиационного поля в разорванной облачности. Для дальнейшего развития теории переноса излучения в облачных полях со стохастической геометрией необходимы комплексные натурные измерения интегральных и спектральных потоков , полей яркости, а также статистических характеристик, описывающих геометрию облачного поля, с максимально возможным контролем оптико-метеорологических параметров системы «атмосфера-подстилающая поверхность».[ ...]
Рисунки к данной главе:
| Корреляционные функции закрытости зенита облаками (/, 2) и нерассеян ного солнечного излучения (1,3) при о = 30 км"1 , D = 1 км, Я = 0,5 км, N = 0,5, £;о = 5° |
 |
| Зависимость от балла облачности средней интенсивности (/, 2) и дисперсии (3 |
 |
| Зависимость дисперсии потока прямой радиации от балла облачности |
 |
| Зависимость среднего потока суммарной радиации от балла облачности при а = 25 км-1, D = = 1км, Н = 0,5 км и Ь-л=50° |
 |
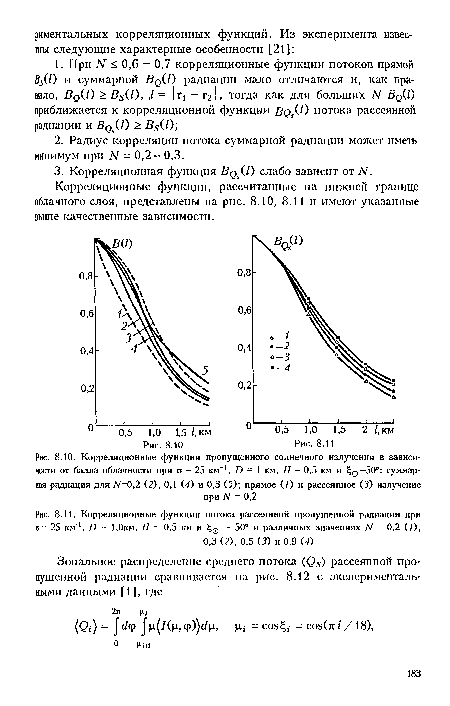
| Корреляционные функции потока рассеянной пропущенной радиации при о = 25 км 1, D = 1,0км, Я = 0,5 км и = 50° и различных значениях N = 0,2 (/), |
 |
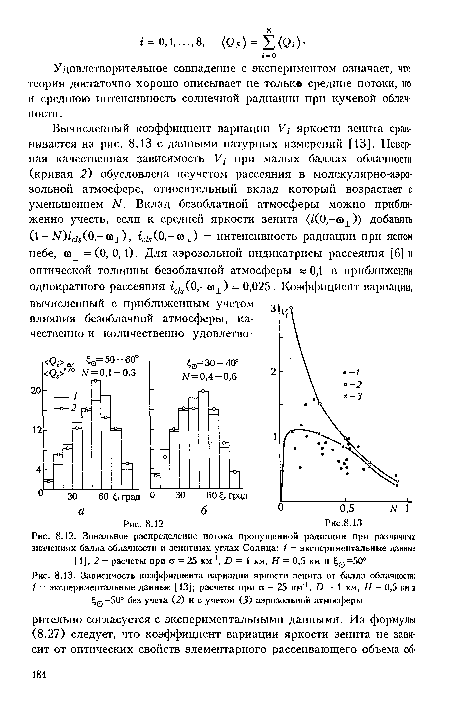
| Зональное распределение потока пропущенной радиации при различных значениях балла облачности и зенитных углах Солнца |
 |
| Зависимость коэффициента вариации яркости зенита от балла облачности |
 |