Выберем систему координат ОХУЕ так, что 2=0 - минимальная, а г = к - максимальная высоты уровня конденсации, г = Н - максимальная высота уровня свободной конвекции. Основания облаков лежат в пределах слоя 0 < г < Л, V - цилиндр высоты к, к «Я, т.к. высота уровня конденсации незначительно изменяется в пространстве [23].[ ...]
Далее будем считать, что фигуры, аппроксимирующие геометрию отдельного облака, имеют одинаковые размеры и форму, например сферы, опрокинутые усеченные параболоиды вращения, цилиндры, кубы и т. д. Фигуры Г могут пересекаться, образуя более сложные конфигурации.[ ...]
Формулы для моментов более высокого порядка имеют аналогичную структуру, весьма громоздки и неудобны для анализа.[ ...]
Существует другой способ разбиения пространства на выпуклые области, связанный с понятием о случайных мозаиках [16, 24, 33]. Мозаики - это совокупность ограниченных выпуклых многогранников, которые, не перекрываясь, покрывают пространство. Определим случайные мозаики, порождаемые пуассоновскими точечными процессами (рис. 6.3).[ ...]
Пусть Р Ц = 1, 2, ..., п) - множество точек, равномерно распределенных в достаточно большом объеме V с плотностью п точек на единицу объема. Разобьем V на клетки по следующему правилу: клетка С/ содержит все точки пространства, ближайшие к Р по сравнению с другими точками Р/(г у). Тогда С/ будет почти наверное выпуклым многогранником, так как является пересечением нескольких плоскостей. Точка Р называется центром клетки С . Множество точек, для которых ближайший центр не является единственным, имеет меру нуль и исключается из рассмотрения. Алгоритм построения облачного поля очевиден: с вероятностью р случайная мозаика является облаком и с вероятностью 1 -р безоблачным промежутком. Если мозаики строят’ся на плоскости, то облака имеют форму цилиндров одинаковой высоты Н, основанием которых является случайный многоугольник. Сведения о статистических характеристиках случайных мозаик приведены в [16, 24, 33].[ ...]
Данная модель является частным случаем более общих моделей случайных полей, связанных с точечными потоками Пальма [27].[ ...]
Отметим, что при выводе (6.19) мы не использовали предположение о том, что точки р/ находятся на одной прямой, они могут быть расположены на произвольной ломаной линии с выполнением неравенств типа (6.18). Это означает, что в данной модели на последовательность точек накладываются значительно менее жесткие требования, чем в модели на пуассоновских потоках точек в пространстве.[ ...]
Выборочные реализации индикаторных полей, построенных на пуассоновскпх ансамблях точек в пространстве и на прямых сильно различаются. Однако, как будет показано ниже (гл. 9), средние характеристики оптического излучения, модулированного статистически однородными облачными полями с соответствующим образом согласованными входными параметрами, отличаются несущественно.[ ...]
Рисунки к данной главе:
| Схематическая иллюстрация модели разорванной облачности, генерируемой пуассоновским ансамблем точек |
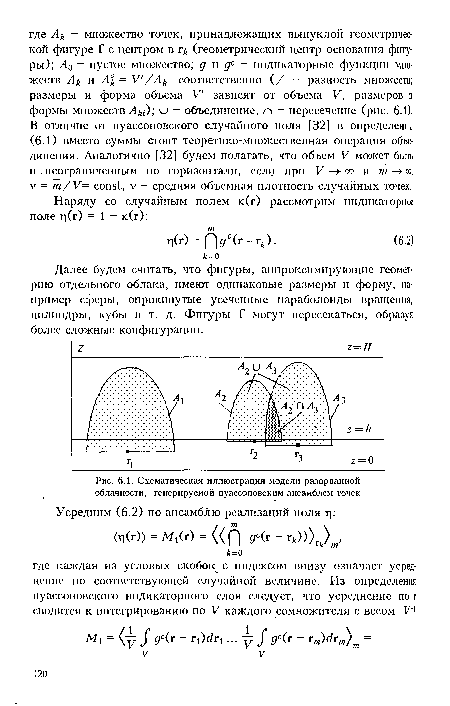 |
| Реализация облачного поля в области 25x25 км2 (вид сверху). Отдельные облака аппроксимируются параболоидами вращения и имеют экспоненциальную функцию распределения по размерам |
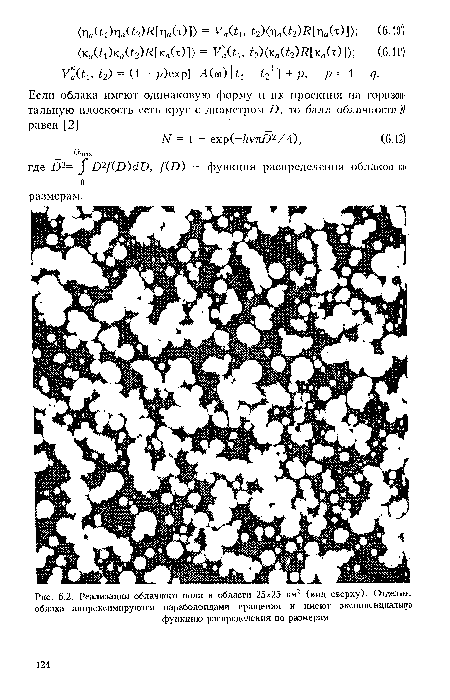 |
| Реализация облачного поля, генерируемого пуассоновскими потоками точек на прямых, в области 25x25 км2 (вид сверху) |
 |