Коэффициенты, дающие оптимальное соответствие с данными для НгО, О О, Нг180, 02180 и ТгО, приведены в табл. 4.3. Стандартная ошибка уравнения (4.6) меньше точности вычисления самих данных.[ ...]
Это выражение характеризует данные при температурах от О до 150° С с точностью 0,04 • ¡О-6 бар-1.[ ...]
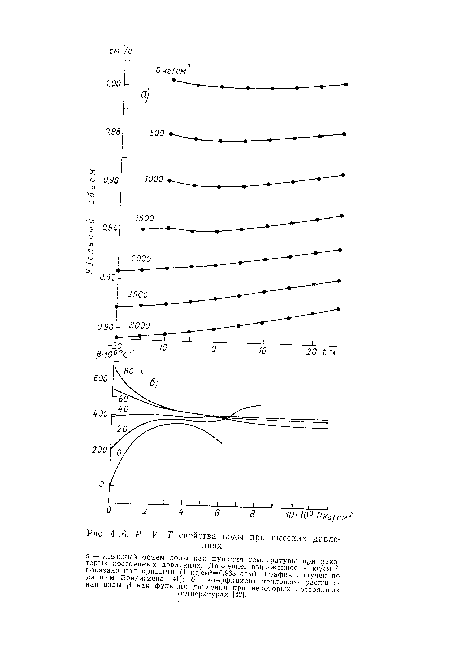
Зависимость теплового расширения воды от давления также является сложной (рис. 4.16 б). При 0°С коэффициент теплового расширения увеличивается по мере сжатия воды до 4000 кг/см2, но при дальнейшем сжатии уменьшается. Тепловое расширение почти не зависит от давления при температуре 40° С. При более высоких температурах оно уменьшается с повышением давления, как и тепловое расширение большинства веществ. Бриджмен, резюмируя влияние сжатия на термодинамические свойства воды, сказал, что вода становится «нормальной жидкостью» при высоком давлении.[ ...]
Молекулярные основы свойств Р—V—Т. Основываясь на данных о плотности воды и о структуре льда I, Бернал и Фаулер [23] предположили, что вода должна иметь более открытую структуру, чем неупорядоченные, плотно упакованные структуры простых жидкостей, таких, как аргон и неон. Они отметили, что межмолекулярное расстояние молекул воды во льду I составляет около 2,8 А, что соответствует «молекулярному радиусу» приблизительно 1,4 А. Неупорядоченный, плотно упакованный ансамбль молекул с радиусом 1,4 А будет иметь плотность 1,84 г/мл. Следовательно, для объяснения наблюдаемой плотности воды, равной 1,0 г/мл, надо исходить из предположений, что либо жидкая вода является плотно упакованной жидкостью, в которой эффективный молекулярный радиус увеличивается от 1,4 А во льду до 1,72 А в воде, либо укладка молекул имеет значительно более открытый характер в воде, чем в плотно упакованных жидкостях. Бернал и Фаулер исходя из рентгенографической картины воды вынуждены были отказаться от первого предположения (см. п. 4.2.1). Как отмечалось выше, они приписали относительно открытую структуру воды наличию широко распространенной четверной координации молекул в жидкости.[ ...]
Эффект 1 является преобладающим при температуре ниже 4° С. где тепловое расширение отрицательно, а эффект 2 преобладает при температуре выше 4° С.[ ...]
Можно рассматривать эти два эффекта как конфигурационный и колебательный вклады в коэффициент теплового расширения. Эффект 1 соответствует конфигурационному вкладу, так как он связан с изменениями средней конфигурации молекул при нагревании воды. Этот вклад в величину [3 является отрицательным. Эффект 2 соответствует колебательному вкладу в величину 3 и имеет положительный знак, а при температуре выше 4° С больше по величине, чем конфигурационный вклад.[ ...]
Рассмотрим, как эти эффекты трактуются в исследованиях, основанных на различных моделях структуры воды (см. п. 4.2.2 и раздел 5).[ ...]
Смешанные модели (например, Грьётгейм и Крог-Мое [134] и Немети и Шерага [252]). Предполагается, что кластеры, образованные при помощи водородных связей, имеют больший молярный объем, чем вода, не содержащая водородных связей. Следовательно, превращение кластеров в молекулы, не соединенные водородными связями, по мере нагревания воды приводит к отрицательному значению величины ДV и соответствует эффекту 1. Колебательное тепловое расширение как кластеров, так и молекул, не соединенных водородными связями, объясняет эффект 2.[ ...]
Бриджмен [42] утверждал, что смешанная модель может полностью объяснить температурную зависимость молярного объема при высоком давлении (рис. 4.16 а). При этом предполагается, что кластеры являются более сжимаемыми, чем остальная жидкость. По мере увеличения давления молярный объем кластеров приближается к объему остальной жидкости, и эффект 1 становится менее выраженным. В результате объемы двух компонентов могут быть одинаковыми, и тогда жидкость показывает нормальное тепловое расширение.[ ...]
Слие и другие [330] вычислили на основании ультразвуковых измерений смеси глицерин—вода, что конфигурационный вклад в т чистой воды составляет около 64% наблюдаемого у’т при 0°С. Дэвис и Литовитц [80] вычислили сходную величину конфигурационного вклада с помощью смешанной модели воды.[ ...]
Рисунки к данной главе:
| Коэффициент изотермической сжимаемости ут жидкой воды при давлении 1 агм [185]. |
![Коэффициент изотермической сжимаемости ут жидкой воды при давлении 1 агм [185].](/static/pngsmall/318625276.png) |
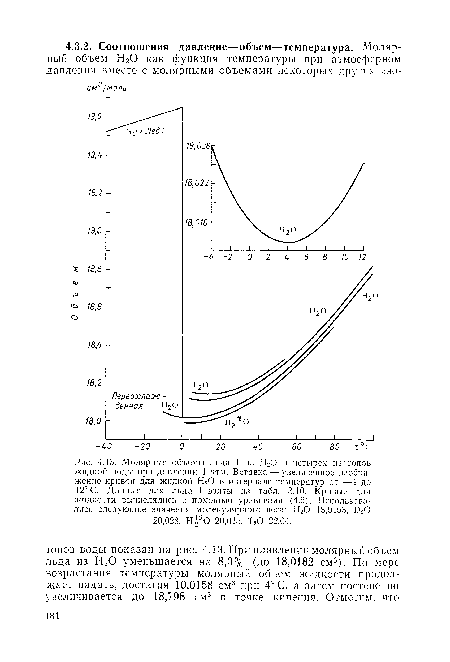
| Рис. 4.16. Р—V—Т свойства воды при высоких давлениях. |
 |
![Коэффициент теплового расширения при постоянном давлении ß льда I и жидкой воды при давлении 1 атм. Заштрихован участок отрицательных значений ß. Ось температуры сокращена ниже 0°С. Данные для льда I взяты из табл. 3.10 и из работы [75], а для жидкой воды — из обзора [185].](/static/pngsmall/318625274.png)