Для изучения свойств математических моделей используют различные методы. Исследуя математическую систему, часто можно догадаться о соответствующих свойствах реальной системы. Основной интерес представляют вопросы обратной связи и регуляции, устойчивости и чувствительности одной части системы к изменениям в другой ее части.[ ...]
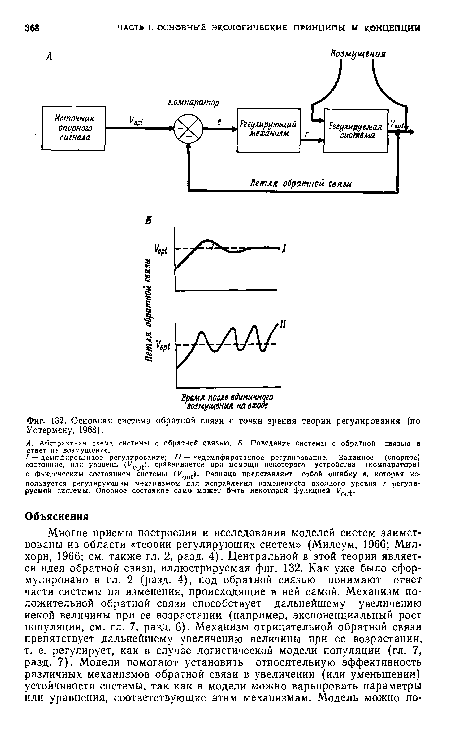
А. Абстрактная схема системы с обратной связью. Б. Поведение системы с обратной связью в ответ на возмущение.[ ...]
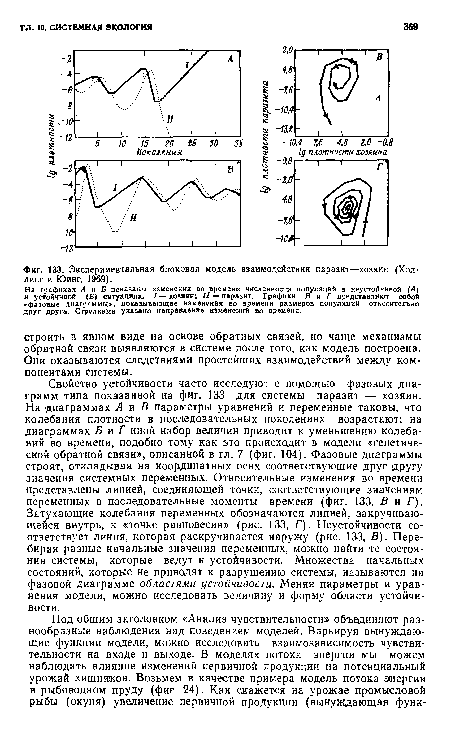
На графиках А и Б показаны изменения во времени численности популяций в неустойчивой (А) и устойчивой (£) ситуациях, / — хозяин; // — паразит. Графики В и Г представляют собой «фазовые диаграммы», показывающие изменения во времени размеров популяций относительно друг друга. Стрелками указано направление изменений во времени.[ ...]
Свойство устойчивости часто исследуют с помощью фазовых диаграмм типа показанной на фиг. 133 для системы паразит — хозяин. На диаграммах А и В параметры уравнений и переменные таковы, что колебания плотности в последовательных поколениях возрастают; на диаграммах Б и Г иной набор величин приводит к уменьшению колебаний во времени, подобно тому как это происходит в модели «генетической обратной связи», описанной в гл. 7 (фиг. 104). Фазовые диаграммы строят, откладывая на координатных осях соответствующие друг другу значения системных переменных. Относительные изменения во времени представлены линией, соединяющей точки, соответствующие значениям переменных в последовательные моменты времени (фиг. 133, В и Г). Затухающие колебания переменных обозначаются линией, закручивающейся внутрь, к «точке равновесия» (рис. 133, Г). Неустойчивости соответствует линия, которая раскручивается наружу (рис. 133, В). Перебирая разные начальные значения переменных, можно найти те состояния системы, которые ведут к устойчивости. Множества начальных состояний, которые не приводят к разрушению системы, называются на фазовой диаграмме областями устойчивости. Меняя параметры и уравнения модели, можно исследовать величину и форму области устойчивости.[ ...]
Другой тип чувствительности — это чувствительность компонентов модели друг к другу, она измеряется: 1) как изменение равновесного значения или средней величины одного компонента при изменении другого; 2) как устойчивость одного в зависимости от устойчивости другого. Например, в модели круговорота питательных веществ (фиг. 21) можно стимулировать какое-либо изменение величины компонента потребления растений и ждать, как это скажется на детритном компоненте. Наконец, мы можем рассматривать чувствительность общих характеристик системы (устойчивость, равновесные значения и т. п.) к изменениям ее параметров и уравнений. Такого рода анализ чувствительности особенно полезен тем, что он указывает области, в которых необходимы более тщательные полевые измерения и экспериментальные проверки. При анализе сложных систем часто выявляются ключевые компоненты или взаимодействия. Можно считать, что эти ключевые факторы находятся в точках схождения сети линий, выражающих причинно-следственные взаимодействия между компонентами системы. В общем анализ чувствительности представляет собой хороший подход в тех случаях, когда стратегия исследования неизвестна или когда нужно выбрать стратегию, приводящую к желаемому результату. Изменяя веса разных компонентов некоторым выбранным заранее способом, можно видеть, какие именно, компоненты модели чувствительны к каждому изменению.[ ...]
Рисунки к данной главе:
| Основная система обратной связи с точки зрения теории регулирования (по Уотермену, 1968). |
 |
| Экспериментальная блоковая модель взаимодействия паразит—хозяин (Холдинг и Юинг, 1969). |
 |