Пользуясь последним выражением, можно вычислить показатель г по данным двух измерений величины популяции (Ыо и Ыг или вообще в любые два момента времени в фазе нелимитированного роста; в этом случае в приведенном уравнении вместо N о и Мг надо подставить величины N1 и А 2, а вместо — разность /2—( ).[ ...]
Общая скорость роста популяции в отсутствие лимитирующего влияния среды (г) зависит от возрастного состава и вклада в репродукцию различных возрастных групп. Таким образом, вид может характеризоваться несколькими величинами г в зависимости от структуры популяции. Когда устанавливается стационарное и стабильное распределение возрастов, специфическую скорость роста называют показателем потенциального роста популяции или Гтах- Часто эту максимальную величину г называют иначе — биотический или репродуктивный потенциал. Разность между гтах, или биотическим потенциалом, и фактической скоростью роста в данных лабораторных или полевых условиях используют как меру сопротивления среды, которая характеризует сумму всех лимитирующих факторов среды, препятствующих реализации биотического потенциала.[ ...]
Лотка (1925), Даблин и Лотка (1925), Лесли и Рэнсон (1940), Берч (1948) и другие выразили это довольно широкое представление о биотическом потенциале посредством математических терминов, понятных на любом языке (однако подчас лишь с помощью хороших математиков!). Хорошо сказал по этому поводу Бирч (1948): «Если попытаться количественно выразить «биотический потенциал» Чепмена в виде одного показателя, то, по-видимому, лучше всего использовать для этого параметр г, поскольку он характеризует внутренне присущую животным способность к увеличению численности при отсутствии лимитирующих влияний среды». Как будет отмечено далее, показатель г часто используется также для количественного выражения «репродуктивной приспособленности» в генетическом смысле.[ ...]
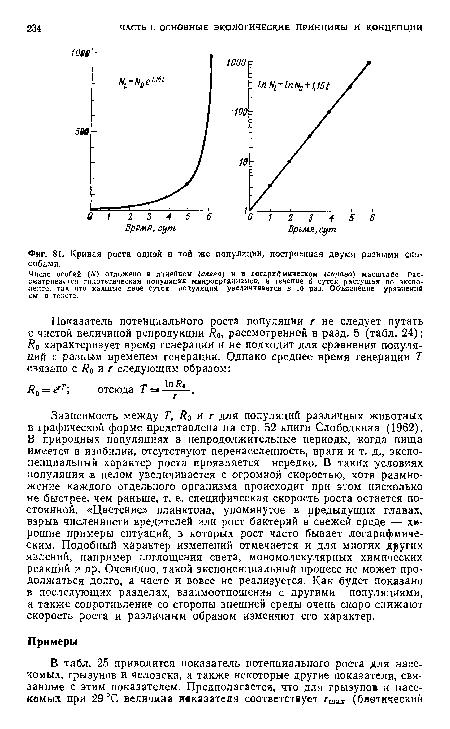
Число особей (ДО отложено в линейном (слева) и в логарифмическом (справа) масштабе. Рассматривается гипотетическая популяция микроорганизмов, в течение 6 суток растущая по экспоненте, так что каждые двое суток популяция увеличивается в 10 раз. Объяснение уравнений см в тексте.[ ...]
Зависимость между Т, Яо и г для популяций различных животных в графической форме представлена на стр. 52 книги Слободкина (1962). В природных популяциях в непродолжительные периоды, когда пища имеется в изобилии, отсутствуют перенаселенность, враги и т. д., экспоненциальный характер роста проявляется нередко. В таких условиях популяция в целом увеличивается с огромной скоростью, хотя размножение каждого отдельного организма происходит при этом нисколько не быстрее, чем раньше, т. е. специфическая скорость роста остается постоянной. «Цветение» планктона, упомянутое в предыдущих главах, взрыв численности вредителей или рост бактерий в" свежей среде — хе-рошие примеры ситуаций, в которых рост часто бывает логарифмическим. Подобный характер изменений отмечается и для многих других явлений, например поглощения света, мономолекулярных химических реакций и др. Очевидно, такой экспоненциальный процесс не может продолжаться долго, а часто и вовсе не реализуется. Как будет показано в последующих разделах, взаимоотношения с другими популяциями, а также сопротивление со стороны внешней среды очень скоро снижают скорость роста и различным образом изменяют его характер.[ ...]
Предельная частота воспроизводства к = ет 1п 1 = г.[ ...]
Рисунки к данной главе:
| Кривая роста одной и той же популяции, построенная двумя разными способами. |
 |