Экология СПРАВОЧНИК

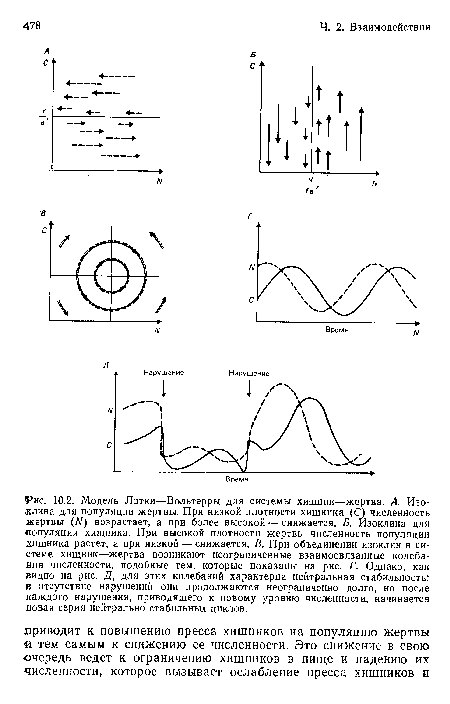
Уравнения Лотки—Вольтерры, для жертвы и для хищника. — При изучении свойств модели полезно провести изоклины. — Модель дает бесконечные, нейтрально устойчивые колебания численности, которые обусловлены присущей популяциям хищник—жертва тенденцией к сопряженным осцилляциям.[ ...]

Простейшая модель, основанная на дифференциальных уравнениях, названа (как и модель межвидовой конкуренции) по имени ее создателей, исследователей Лотки и Вольтерры (Lotka, 1925; Volterra, 1926). Эта модель крайне упрощена, но она полезна в качестве отправной точки. Модель состоит из двух компонентов: С — численность популяции консумента( = хищник) и N — численность или биомасса популяции жертвы или растений.[ ...]

Численность зайца, тыс.[ ...]

Уравнения 10.1 и 10.2 и составляют модель Лотки—Вольтерры.[ ...]

Таким образом, поскольку г и а константы, изоклиной для жертвы будет линия, для которой величина С является постоянной (рис. 10.2, Л).[ ...]

Картину, полученную на модели, не следует, однако, воспринимать слишком серьезно. Для нее характерна «нейтральная стабильность», которая означает, что популяции неограниченно долго совершают один и тот же цикл колебаний до тех пор, пока какое-либо внешнее воздействие не изменит их численность, после чего популяции совершают новые циклы неограниченных колебаний (рис. 10.2, Д). На самом деле среда, конечно, постоянно меняется и численность популяций будет постоянно «смещаться на новый уровень». Следовательно, популяция, которая ведет себя в соответствии с моделью Лотки—Вольтерры,. будет испытывать неустойчивые колебания. Как только популяция вступит в очередной цикл, она будет переведена в новый режим. Чтобы циклы колебаний, которые совершает популяция, были регулярными и распознаваемыми, они должны быть стабильными: если внешнее воздействие изменяет уровень численности популяций, то они должны стремиться вернуться к первоначальному циклу. Такие циклы, в отличие от нейтрально устойчивых колебаний в модели Лотки—Вольтерры, принято называть устойчивыми предельными циклами.[ ...]

Модель Лотки—Вольтерры тем не менее полезна в том отношении, что позволяет показать основную тенденцию в отношениях хищник—жертва, которая выражается в возникновении колебаний численности в популяции жертвы, сопровождающихся колебаниями численности в популяции хищника (т. е. в возникновении сопряженных колебаний). Основным механизмом таких колебаний является запаздывание по времени, свойственное последовательности состояния от высокой численности жертв к высокой численности хищников, затем к низкой численности жертв и низкой численности хищников, к высокой численности жертв и т. д. (табл. 10.1).[ ...]

Рисунки к данной главе:

Модель Лотки—Вольтерры для системы хищник—жертва. А. Изоклина для популяции жертвы. При низкой плотности хищника (С) численность жертвы (М) возрастает, а при более высокой — снижается. Б. Изоклина для популяции хищника. При высокой плотности жертвы численность популяции хищника растет, а при низкой — снижается. В. При объединении изоклин в системе хищник—жертва возникают неограниченные взаимосвязанные колебания численности, подобные тем, которые показаны на рис. Г. Однако, как видно на рис. Д, для этих колебаний характерна нейтральная стабильность