Модель свидетельствует о том, что внутривидовая конкуренция может привести к самым различным колебаниям численности популяции. — Запаздывание по времени, предшествующее изменению численности.[ ...]
Еще одним положительным качеством, которое, так же как и другим хорошим моделям, свойственно уравнению 6.4, является его способность освещать новые стороны реального мира.[ ...]
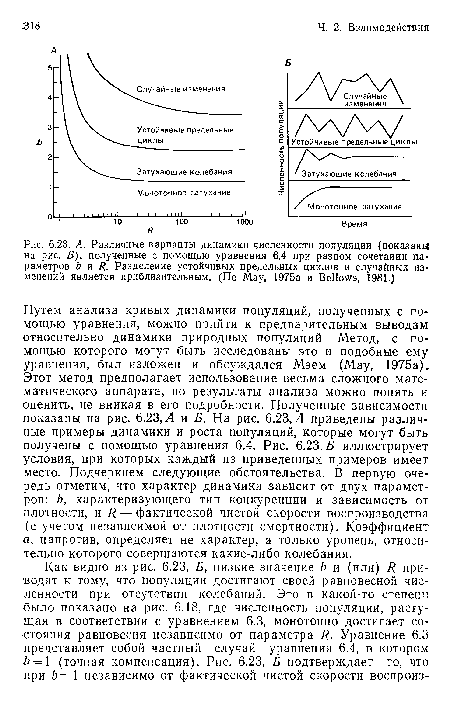
Путем анализа кривых динамики популяций, полученных с помощью уравнения, можно прийти к предварительным выводам относительно динамики природных популяций Метод, с помощью которого могут быть исследованы это и подобные ему уравнения, был изложен и обсуждался Мэем (May, 1975а). Этот метод предполагает использование весьма сложного математического аппарата, но результаты анализа можно понять и оценить, не вникая в его подробности. Полученные зависимости показаны на рис. 6.23, Л и Б. На рис. 6.23, Л приведены различные примеры динамики и роста популяций, которые могут быть получены с помощью уравнения 6.4. Рис. 6.23, Б иллюстрирует условия, при которых каждый из приведенных примеров имеет место. Подчеркнем следующие обстоятельства. В первую очередь отметим, что характер динамики зависит от двух параметров: Ь, характеризующего тип конкуренции и зависимость от плотности, и R — фактической чистой скорости воспроизводства (с учетом независимой от плотности смертности). Коэффициент а, напротив, определяет не характер, а только уровень, относительно которого совершаются какие-либо колебания.[ ...]
По мере увеличения значений Ь и(или) Я численность популяции сначала демонстрирует затухающие колебания, постепенно приводящие к равновесному состоянию, а затем к «устойчивым предельным циклам», в соответствии с которыми популяция колеблется около состояния равновесия, неоднократно проходя при этом через те же самые две, четыре или даже большее число точек. И наконец, при самых высоких значениях Ь и Я колебания численности популяции имеют полностью нерегулярный и хаотический характер.[ ...]
Таким образом, модель, в основу которой положен зависимый от плотности процесс (внутривидовая конкуренция), предположительно обладающий регуляторными свойствами, может давать широкое разнообразие типов динамики популяции. Если модельная популяция имеет даже относительно невысокую основную чистую скорость размножения (а особь, оставляющая в следующем поколении 100 ( = ./?) потомков при условии отсутствия конкуренции — явление вполне возможное) и если ее зависимая от плотности реакция приводит даже к небольшой сверхкомпенсации, то численность популяции будет далека от стабильного уровня и может колебаться в широких пределах без воздействия какого-либо внешнего фактора. Биологическое значение этого результата состоит в следующем: он позволяет не без веских оснований предположить возможность возникновения в совершенно постоянной и предсказуемой среде значительных и даже хаотических колебаний численности, связанных только с внутренними свойствами самой популяции и составляющих ее особей. Очевидно, что последствия внутривидовой конкуренции не ограничены только «строго контролируемой регуляцией».[ ...]
По сравнению с этим результатом первоначальное уравнение без запаздывания дает монотонное замедление роста численности при всех значениях Я. Запаздывание по времени приводит к колебаниям численности в модели и, как можно предположить, оказывает сходное дестабилизирующее влияние на реальные популяции (см. также разд. 10.2.2).[ ...]
Из настоящего раздела следует сделать два важных вывода. Первый заключается в том, что запаздывание по времени, высокая скорость размножения и сверхкомпенсация при существовании зависимости от плотности в состоянии (по отдельности или совместно) вызвать все типы колебаний плотности популяций без участия каких-либо внешних причин. Второй, не менее важный вывод состоит в том, что этот результат получен путем анализа математических моделей.[ ...]
Рисунки к данной главе:
Вернуться к оглавлению