Отсутствие конкуренции: экспоненциальное увеличение численности популяции.— Включение внутривидовой конкуренции.[ ...]
Точка В, напротив, отражает ситуацию, в которой численность популяции (А ) гораздо выше и где в значительной степени существует внутривидовая конкуренция. В самом деле, в точке В фактическая чистая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может не более, чем восстанавливать в каждом поколении свою численность, потому что количество родившихся особей уравновешивается количеством погибших. Другими словами, ЛГ(+1 в точности соответствует и А /Л/ж равно 1, а численность популяции, при которой имеет место это соотношение, называется предельной плотностью насыщения К (рис. 6.5).[ ...]
Это уравнение представляет собой модель роста популяции, ограниченного внутривидовой конкуренцией. Суть этой модели в том, что нереалистичная константа Я в уравнении (6.1) заменена на фактическую чистую скорость воспроизводства, Я/(1 - -a-Nt), которая уменьшается по мере роста численности популяции (ЛГг).[ ...]
Свойства приведенной выше модели можно понять, обратившись к рис. 6.19 (на основе которого модель получена) и рис. 6.18 (на котором показан рост гипотетической популяции во времени в соответствии с моделью). Численность популяции на рис. 6.18 при очень низких значениях Nt растет экспоненциально, но с увеличением численности скорость роста все более снижается, до тех пор пока численность не достигнет предельной плотности насыщения и скорость будет равна нулю; в результате получается Э-образная или сигмоидная кривая. Такой результат представляется реалистичным, но при этом следует иметь в виду, что существует много других моделей, которые также дают подобную кривую. Преимущество уравнения (6.3) в его простоте. Для того чтобы лучше понять поведение модели вблизи точки, соответствующей предельной плотности насыщения, обратимся к рис. 6.19. При численности, меньшей К, популяция будет расти; при численности, большей К, популяция будет уменьшаться, а при численности, равной К, — оставаться на постоянном уровне. Таким образом, предельная плотность насыщения характеризует положение устойчивого равновесия популяции, а модель отражает регуляторные свойства, которые считаются присущими внутривидовой конкуренции.[ ...]
На рис. 6.20 приведено несколько кривых зависимости Ь. от при разных значениях а, введенных в модель. Во всех случаях наклон кривой достигает 1 и затем не меняется. Другими словами, зависимость от плотности всегда начинается с неполной компенсации, а затем при более высоких значениях М наблюдается точная компенсация. Таким образом, модель ограничена типом конкуренции, который она имитирует, и пока мы можем сказать только то, что такой тип конкуренции приводит к строго контролируемой регуляции численности популяций.[ ...]
Рисунки к данной главе:
| Простейшая прямолинейная зависимость, в соответствии с которой с возрастанием плотности (А^<) может увеличиваться величина, обратная показателю роста генерации ( Л^/Л^+1). Подробнее см. в тексте |
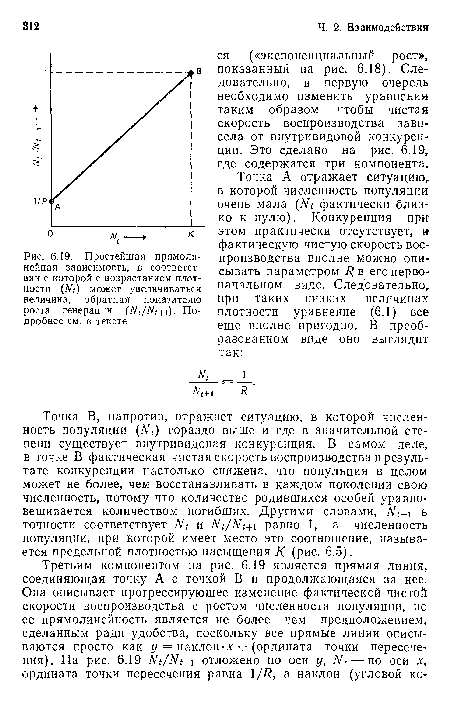 |
| Внутривидовая конкуренция, выраженная уравнением 6.3. Независимо от начальной плотности или константы а=(к— )/К наклон линии, связывающей Л |
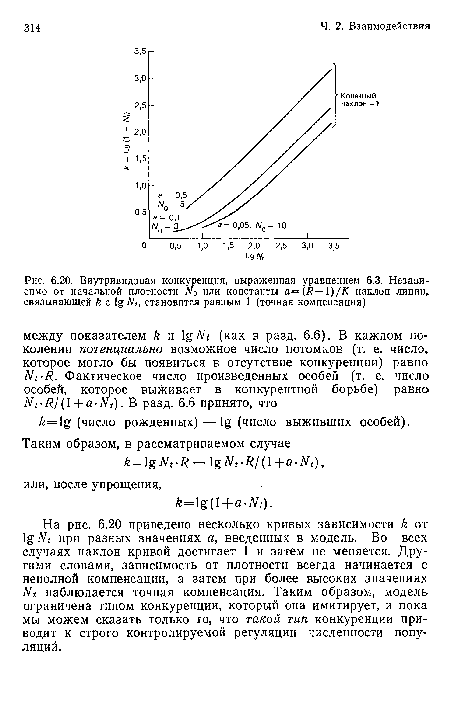 |
| Внутривидовая конкуренция, выраженная уравнением 6.4. Конечный наклон определяется значением Ь в этом уравнении. |
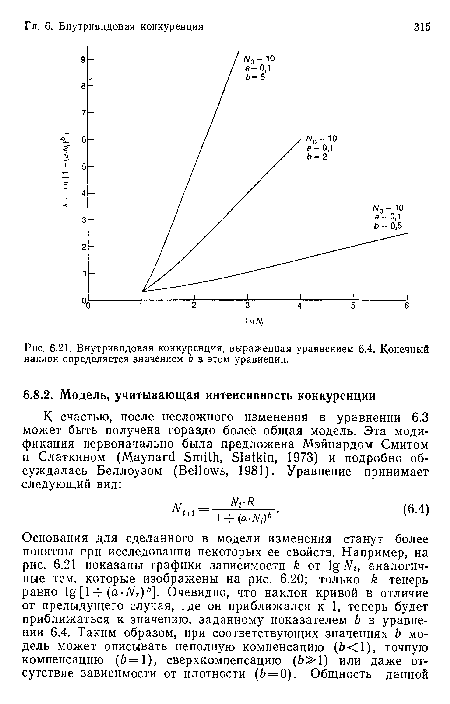 |
Аналогичные главы в дргуих документах:
| См. далее:Основные уравнения |