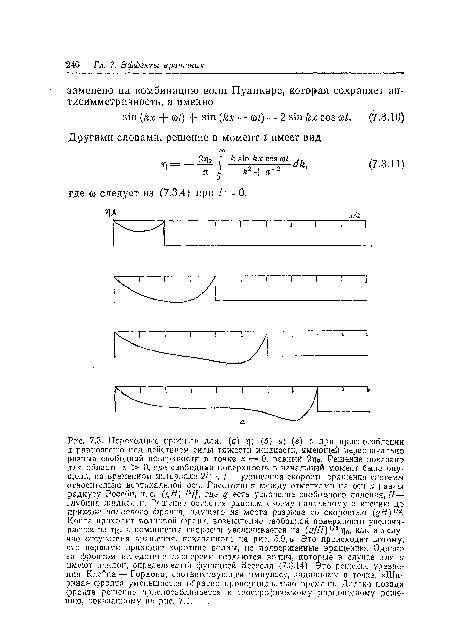
(а) г); (б) u; (s) v при приспособлении К равновесию под действием силы тяжести жидкости, имеющей первоначально разрыв свободной поверхности в точке х — 0, равный 2щ. Решение показано для области А > 0, где свободная поверхность в начальный момент была опущена, на временном интервале 2/->, f — удвоенная скорость вращения системы относительно вертикальной оси. Расстояния между отметками на оси х равны радиусу Россби, т. е. (gH)|/2//. где g есть ускорение свободного падения, Н— глубина жидкости. Решение остается равным своему начальному значению до прихода волнового фронта, идущего из места разрыва со скоростью (gH) Когда приходит волновой фронт, возвышение свободной поверхности увеличивается на г)0, а компонента скорости увеличивается на (g/H)l/2 г 0, как и в случае отсутствия вращения, показанного на рис. 5.9, а. Это происходит потому, что первыми приходят короткие волны, не подверженные вращению. Однако за фронтом вследствие дисперсии создаются волны, которые в случае для и имеют наклон, определяемый функцией Бесселя (7.3.14). Это решение уравнения Клейна — Гордона, соответствующее импульсу, заданному в точке. «Ширина» фронта уменьшается обратно пропорционально времени. Далеко позади фронта решение приспосабливается к геострофпческому равновесному решению, показанному па рис. 7.1.
Вернуться к оглавлению