| Фазовый портрет обобщенной логистической популяции. Вся траектория лежит под прямой dNjdt = F 0)N |
 |
Далее
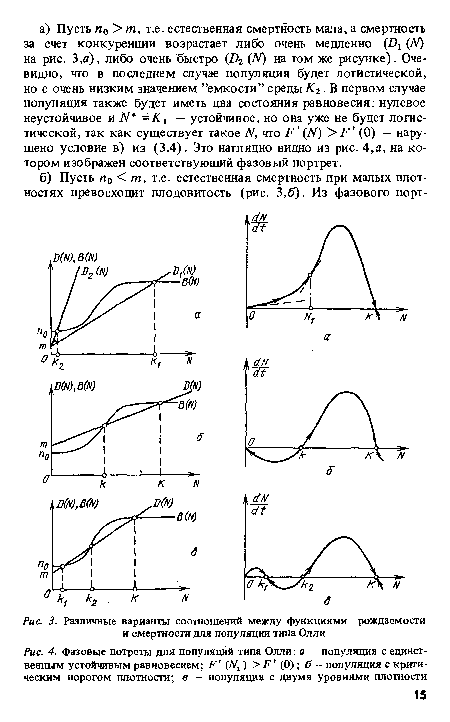
| Различные варианты соотношений между функциями рождаемости и смертности для популяции типа Олли |
 |
Далее
| Фазовый портрет популяции с гиперболическим законом роста - предельный случай Г (0) =0 |
 |
Далее
| Фазовый портрет уравнения (5.16) |
 |
Далее
| Распространение "псевдовол-ны” (сплошными линиями обозначены значения плотностей в локальных ареалах в начальный момент, точками -некоторое время спустя) |
 |
Далее
| Мальтузианские функции при различных значениях у |
 |
Далее
| Зависимость малого параметра е от 7 |
 |
Далее
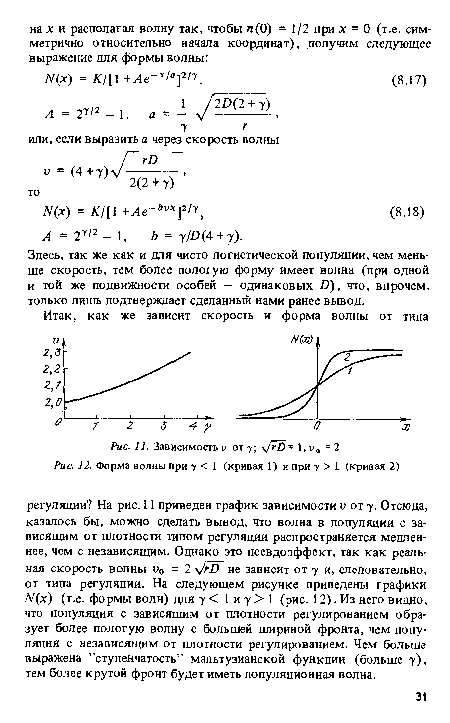
| Форма волны при у < 1 (кривая 1) и при у > 1 (кривая 2) |
 |
Далее
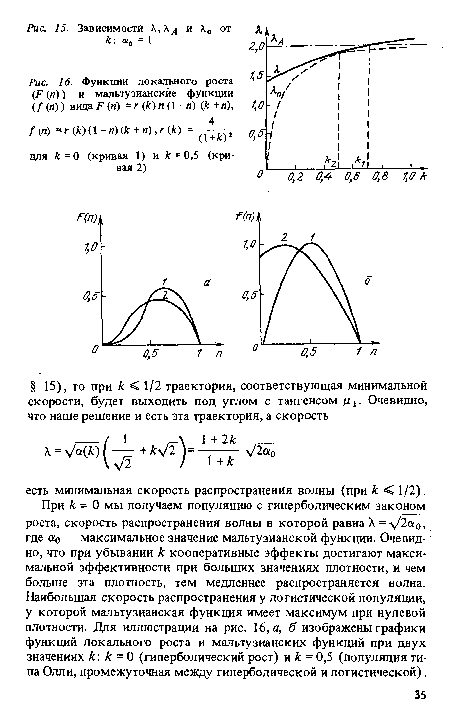
| Функции локального роста (F (ri) ) и мальтузианские функции (/ (л) ) вида F (и) = г (к) п (1 -я) {к + я), 1,0 |
 |
Далее
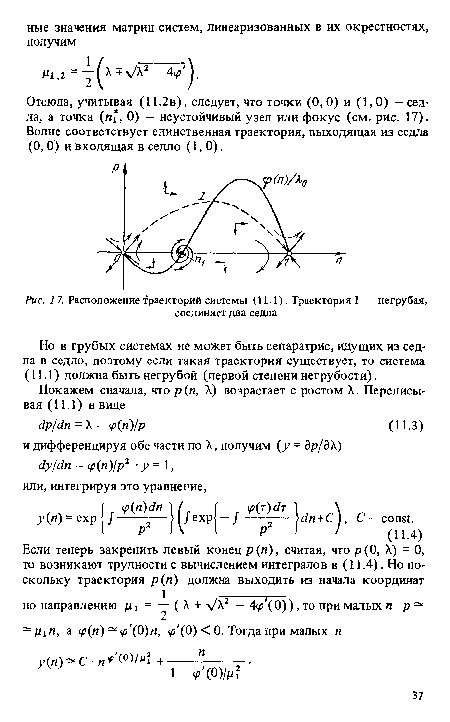
| Расположение траекторий системы (11.1). Траектория I - негрубая, |
 |
Далее
| Поведение траекторий (11.1) при изменении |
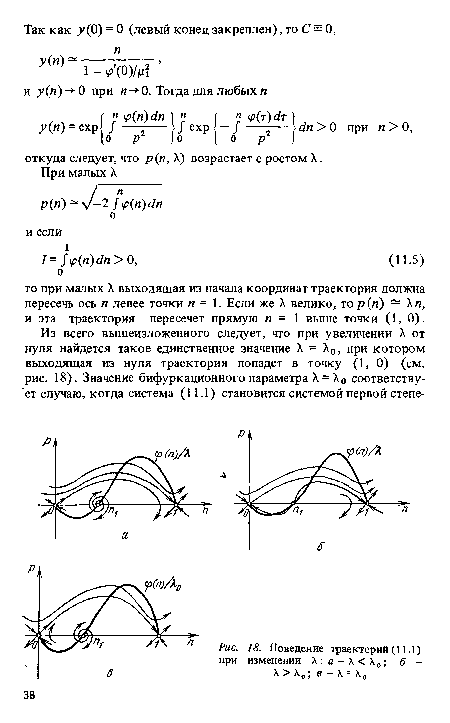 |
Далее
| Расположение траекторий системы (11.1) при - 0 и / # (п) с1п < 0. |
 |
Далее
| Траектории, соответствующие волнам размножения ( 0) и вымирания (А.,) |
 |
Далее
| Распространение волн размножения и вымирания от локальной вспышки (Г„ < Г, < Гг) |
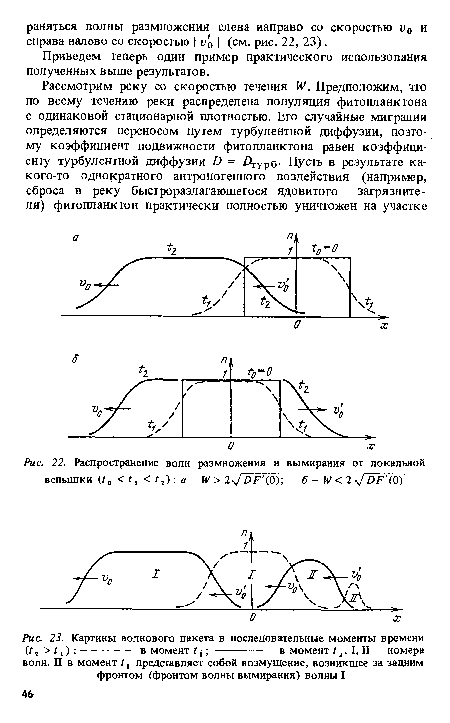 |
Далее
| Картины волнового пакета в последовательные моменты времени |
 |
Далее
| Собственные направления (15.3) в зависимости от знаков и величин |
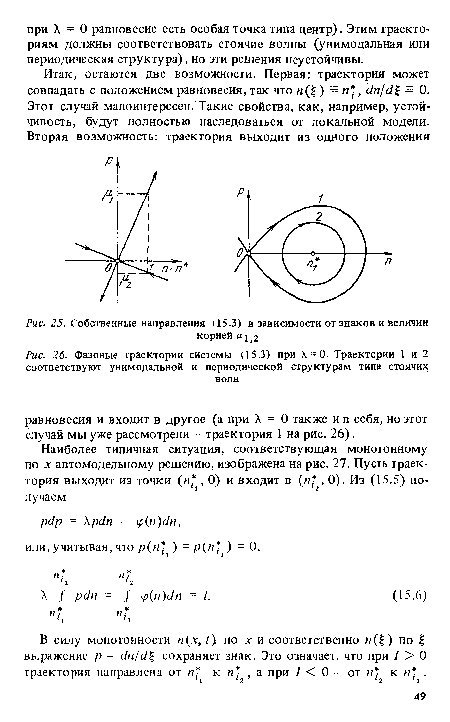 |
Далее
| Фазовые траектории системы (15.3) при = 0. Траектории 1 и 2 соответствуют унимодальной и периодической структурам типа стоячих |
 |
Далее
| Траектория монотонного автомодельного режима в случае двух |
 |
Далее
| Направление движения волны переброса в зависимости от знака |
 |
Далее
| Фазовый портрет системы (15.3) в случае волны переброса от п к п . Траектория 1 соответствует скорости |
 |
Далее
| Трофические функции первого ("глупый” хищник - 1) и второго ("умный” хищник - 2) типов |
 |
Далее
| Форма волны потребителя в системе "неподвижный иевозобновимый ресурс - потребитель”. Она имеет крутой передний и растянутый задний фронт |
 |
Далее
| Форма волны потребителя при различных Я„ Я 0 > ; и, > о2 |
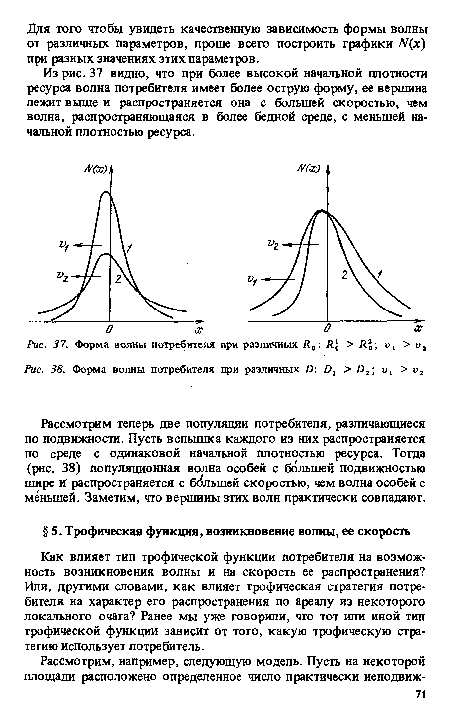 |
Далее
| Форма волны потребителя при различных /> |
 |
Далее
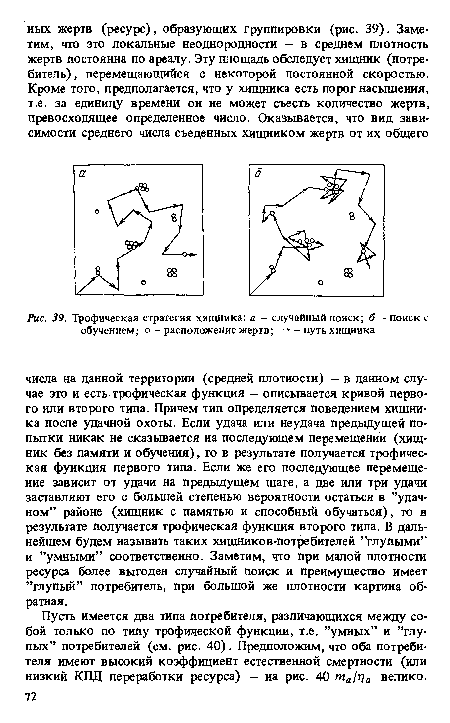
| Трофическая стратегия хищника |
 |
Далее
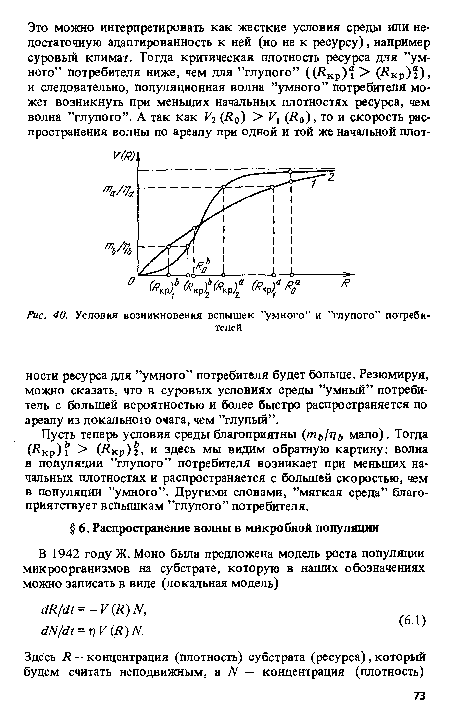
| Условия возникновения вспышек ’’умного” и ’’глупого” потребителей |
 |
Далее
| Поле направлений и расположение траекторий в окрестности особых точек системы (6.6). Прямая т]Л + N = = пЯ0 - изоклина |
![Поле направлений и расположение траекторий в окрестности особых точек системы (6.6). Прямая т]Л + N = = пЯ0 - изоклина](/static/pngsmall/825585054.png) |
Далее
| Возможные типы ограниченных траекторий системы (8.2) |
 |
Далее
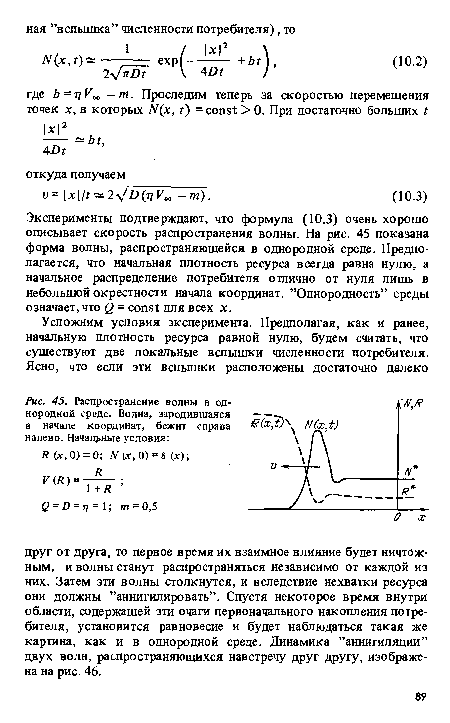
| Распространение волны в однородной среде. Волна, зародившаяся в начале координат, бежит справа налево. Начальные условия |
 |
Далее
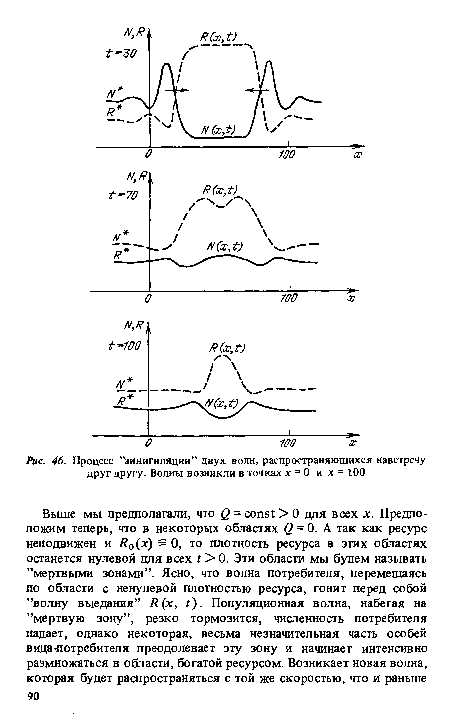
| Процесс ’’аннигиляции” двух волн, распространяющихся навстречу друг другу. Волиы возникли в точках х = 0 и х = 100 |
 |
Далее
| Стационарные распределения ресурса и потребителя, устанавливающиеся в окрестности границы полубес-конечной ’’мертвой зоны” (б = 0 при х < 0, (2=1 при х > 0); |
 |
Далее
| Процесс преодоления волной потребителя "мертвой зоны” (отрезок [0,/]) |
![Процесс преодоления волной потребителя "мертвой зоны” (отрезок [0,/])](/static/pngsmall/825585088.png) |
Далее
| Зависимость скорости распространения волны от мальтузианского параметра (для логистической популяции, р = 50 км/год). Заштрихованные области соответствуют данным, полученным в течение трех вспышек елового почкоеда. Сверху приведены года максимума соответствующих вспышек |
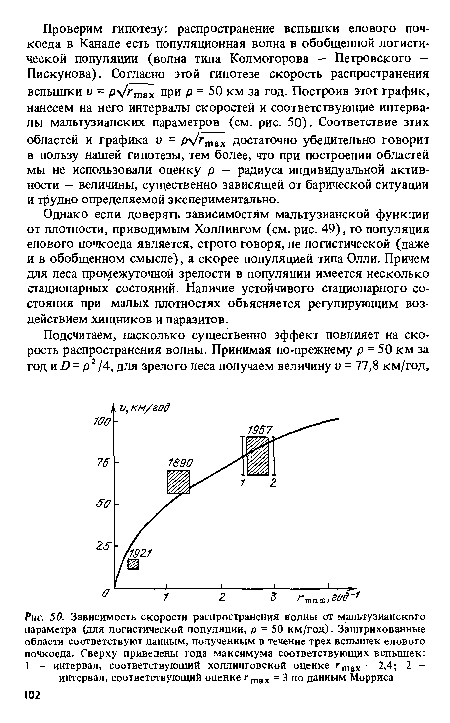 |
Далее
| Гистограмма распределения скоростей распространения вспышки (---- возможный вид аппроксимирующего распределения) |
 |
Далее
| Возможные варианты равновесий в локальной модели эпидемии (о - устойчивое равновесие, • - неустойчивое равновесие) |
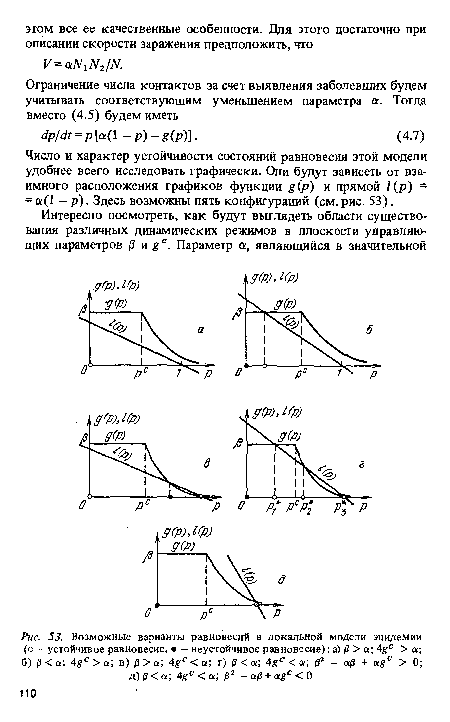 |
Далее
| Области существования различных динамических режимов в плоскости (0, gc) при а = 0,8 |
 |
Далее
| Графики функций локальных изменений генной частоты аллеля А |
 |
Далее
| Средние численности мух еуегмев ловушках через 15 дней после их выпуска в репродуктивном центре (/ =0) (о - экспериментальные |
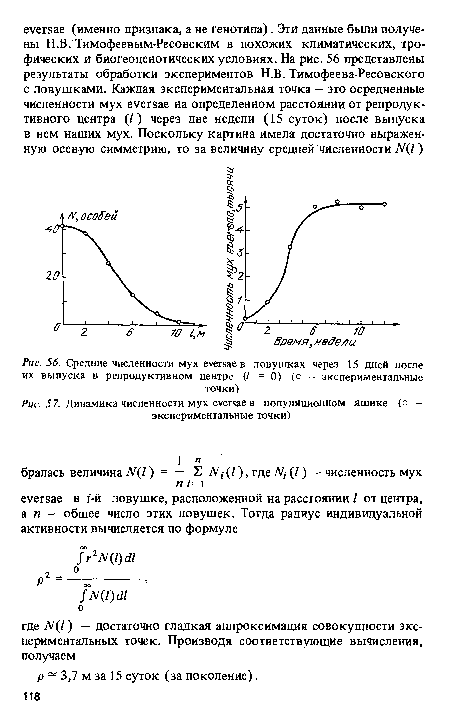 |
Далее
| Динамика численности мух еуетев популяционном ящике (о -экспериментальные точки) |
 |
Далее
| К выбору начального распределения плотности |
 |
Далее
| Картина автомодельной волны с изломом |
 |
Далее
| Решение (4.3) полученное численным методом (б) при начальном распределении (а) |
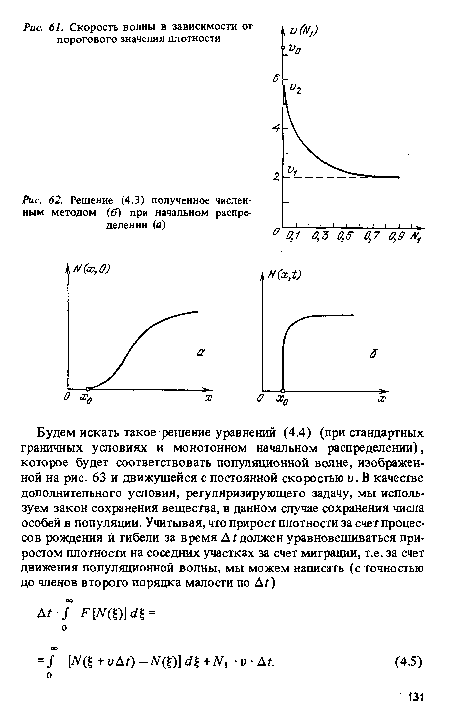 |
Далее
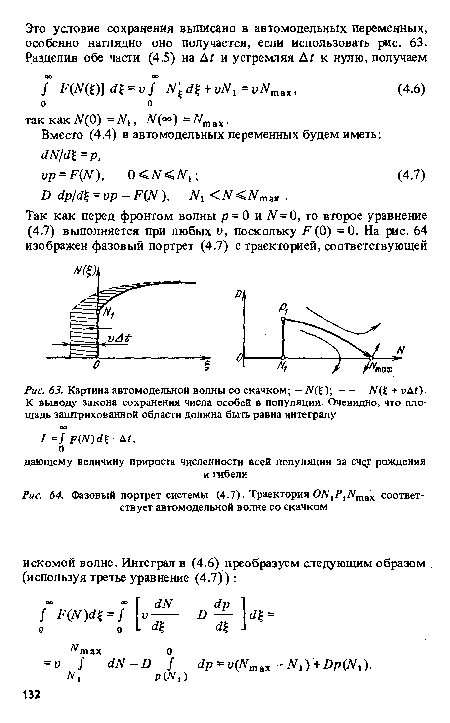
| Картина автомодельной волны со скачком; - ЩЧУ,---N(4 + иДГ). |
 |
Далее
| Фазовый портрет системы (4.7). Траектория ОИ1Р1Итлх соответствует автомодельной волне со скачком |
 |
Далее
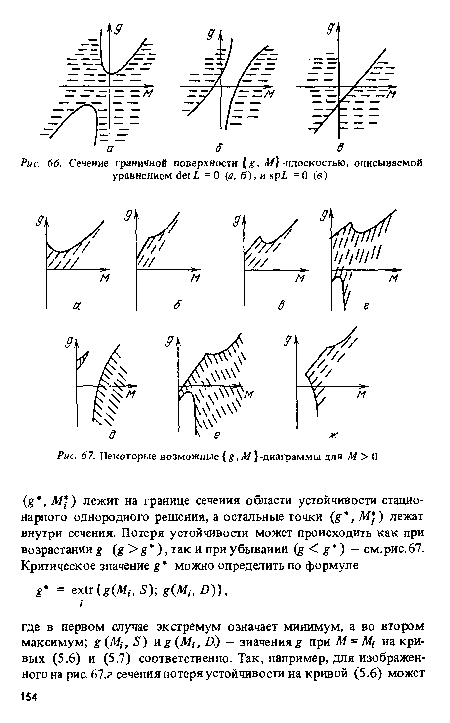
| Некоторые возможные {£,.Л/}-диаграммы для М> 0 |
 |
Далее
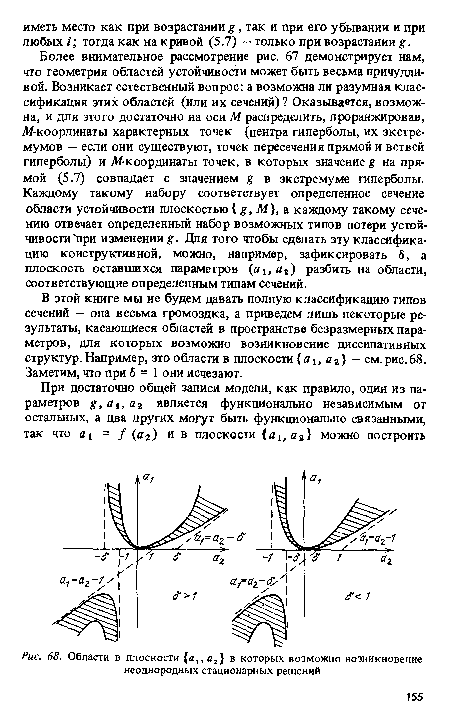
| Области в плоскости {а,, а,} в которых возможно возникновение неоднородных стационарных решений |
 |
Далее
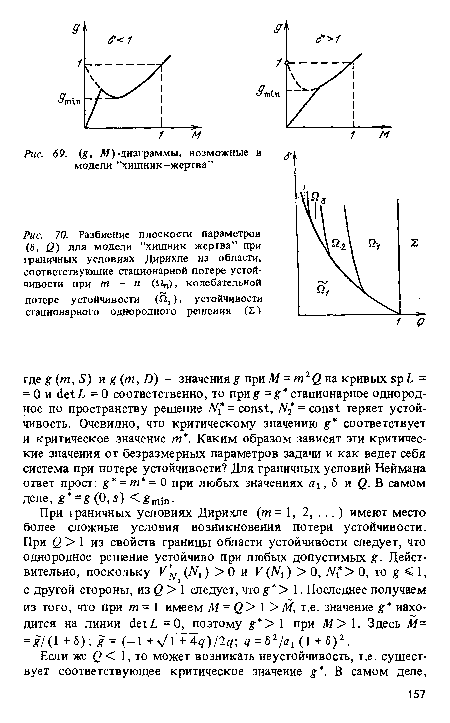
| Разбиение плоскости параметров (8, б) для модели "хищник-жертва” при граничных условиях Дирихле на области, соответствующие стационарной потере устойчивости при т = п (Пп), колебательной потере устойчивости С^), устойчивости стационарного однородного решения (£) |
 |
Далее
| Области в плоскости I —; ——- , в которых возможно возник- |
 |
Далее
| Невыпуклый ареал (область типа гантели), в которой могут существовать неоднородные по пространству стационарные структуры для одной изолированной популяции (а). Для этого нужно, чтобы функция /(Л ), описывающая локальную популяционную динамику, была, как на рис. б. На рис. в изображено начальное распределение, эволюция которого может |
 |
Далее
| Бифуркационные диаграммы для случаев д, 0 (а) и = 0. дг Ф 0 (б, в). Сплошной линией показаны устойчивые ветви решения, а штриховой - неустойчивые |
 |
Далее
| Стационарное устойчивое распределение плотноста жертв - ^1(х , х2).Штриховкой обозначен срез, соответствующий ТУ, |
 |
Далее
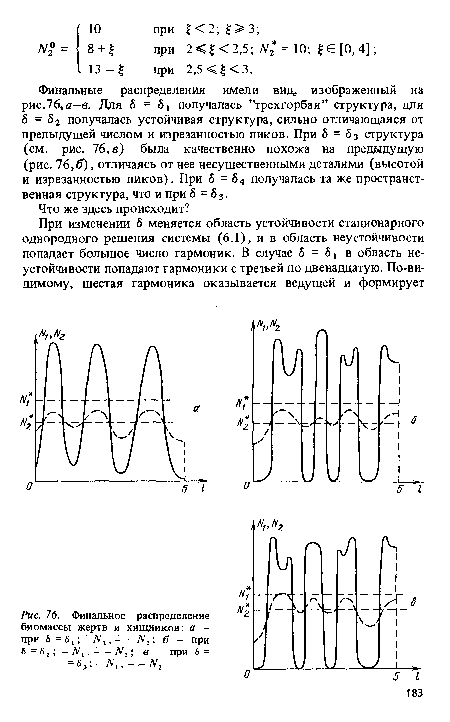
| Финальное распределение биомассы жертв и хищников |
 |
Далее
| Зависимость функции смертности потребителя от его численности |
 |
Далее
| Возможный вид стационарного распределения ресурса R(x) |
 |
Далее
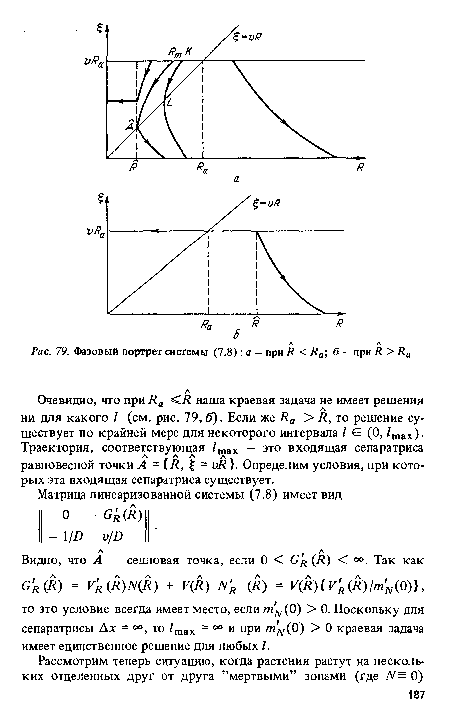
| Фазовый портрет системы (7.8) |
 |
Далее
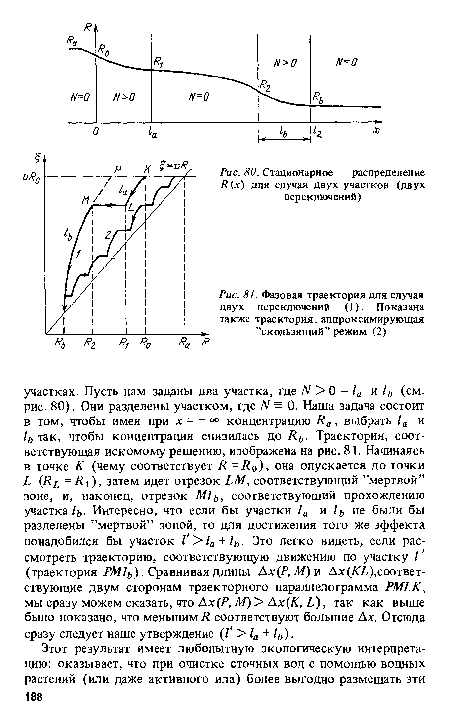
| Фазовая траектория для случая двух переключений (1). Показана также траектория, аппроксимирующая "скользящий” режим (2) |
 |
Далее
| Примерный профиль верхового болота |
 |
Далее
| Зависимость скорости торфо-накопления от уровня болотных воя |
 |
Далее
| Профиль болота в стационарном состоянии (2), для сравнения изображены эллипс (/) и парабола (3) - кривые, применявшиеся ранее для описания профиля болот по эмпирическим данным |
 |
Далее
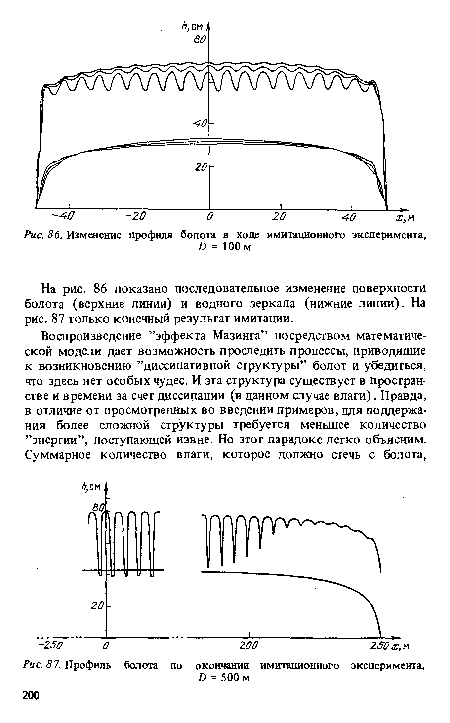
| Изменение профиля болота в ходе имитационного эксперимента, |
 |
Далее
| Профиль болота по окончании имитационного эксперимента, |
 |
Далее
| Область устойчивости однородного решения системы (6.2) (АехАт < <0) |
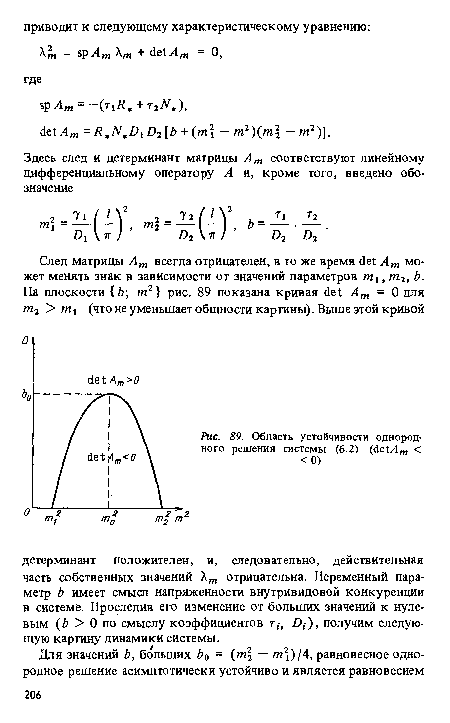 |
Далее
| Перестройка фазового портрета в окрестности равновесия в момент бифуркации |
 |
Далее
| Области параметров, определяющих существование неоднородных решений нелинейной задачи |
 |
Далее
| Примерный вид зависимости мальтузианской функции а О) для популяции типа Олли; х, - неустойчивое равновесие, х - устойчивое равновесие |
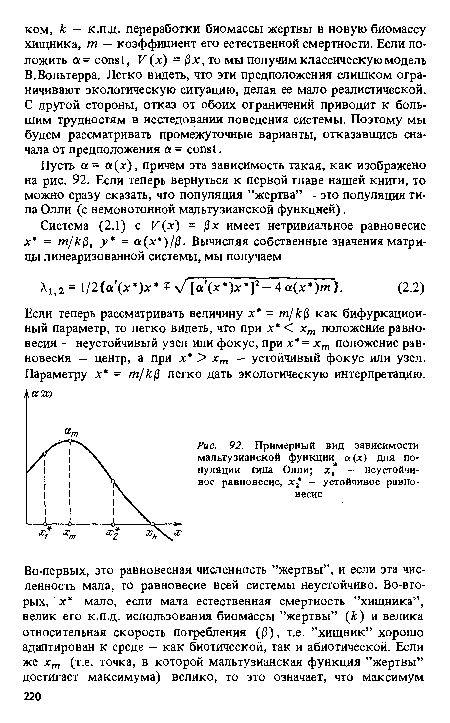 |
Далее
| Зависимость амплитуды стационарных колебаний от параметра от. Из этого графика видно, что система ’’хищник - жертва” - автоколебательная система с мягким самовозбуждением. Точка Хт - критическая, I - устойчивое равновесие, II - устойчивый предельный цикл, III - неустойчивое равновесие |
 |
Далее
| Равновесное многообразие У = F(X) для системы (5.1); 1 - Хк < <ч/27; 2-Хк>^П |
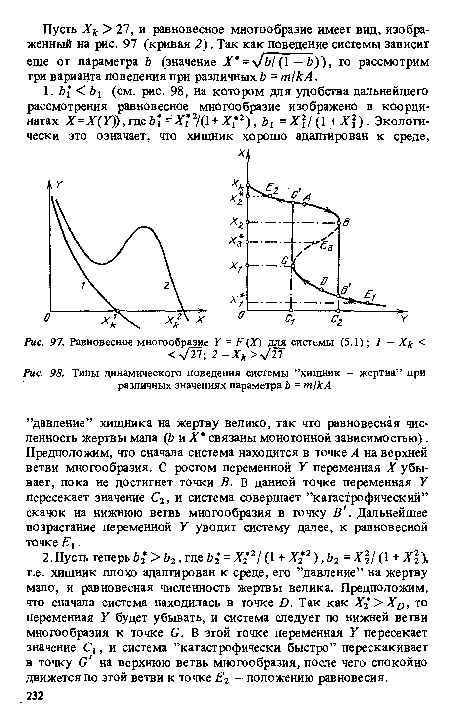 |
Далее
| Типы динамического поведения системы ’’хищник - жертва” при различных значениях параметра Ъ = т/к А |
 |
Далее
| Поверхность X = X(У, Хк) и ее проекция на плоскость { У, Х%} . На кривых С,£, и С, К, отображение имеет особенности типа складки, в точке С, - сборку |
 |
Далее
| Характер динамического поведения системы ’’хищник - жерт- |
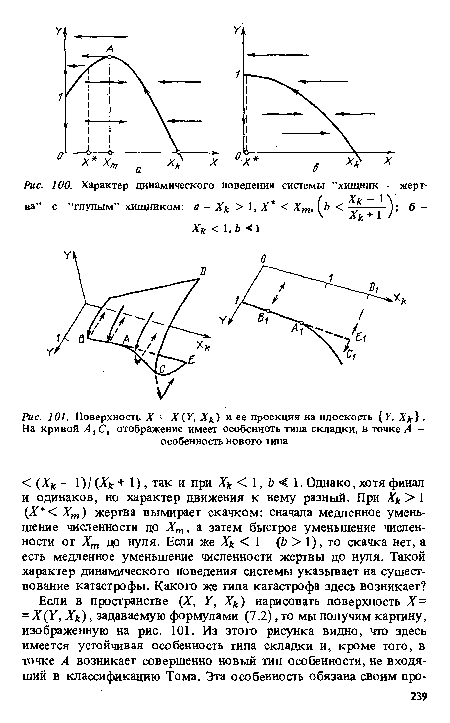 |
Далее
| Сепаратрисы 5,- (/ = 1, 2, 3) системы (3.1) (л = 3) |
 |
Далее
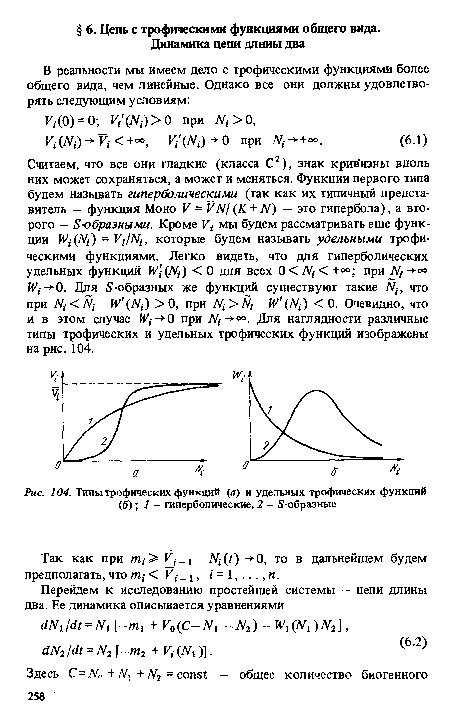
| Типы трофических функций (а) и удельных трофических функций (б); 1 - гиперболические, 2 - 5-образные |
 |
Далее
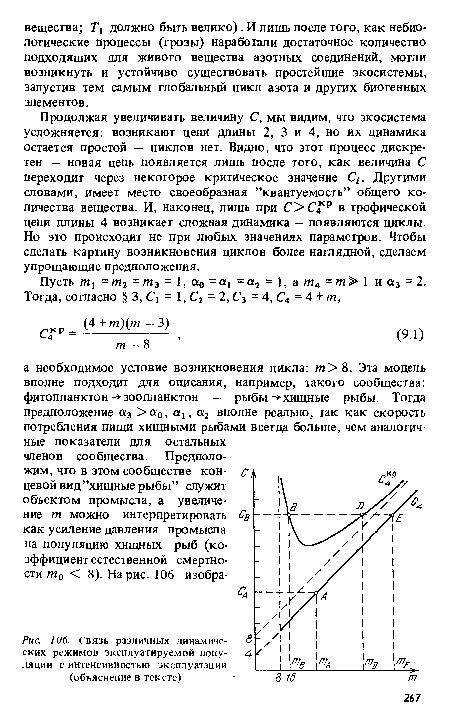
| Связь различных динамических режимов эксплуатируемой популяции с интенсивностью эксплуатации (объяснение в тексте) |
 |
Далее
| Динамика численности полевки Брандта (в относительных единицах) |
 |
Далее
| Области различных динамических режимов системы (2.1); 1 - область предстохастичности, II - область стохастичности |
 |
Далее
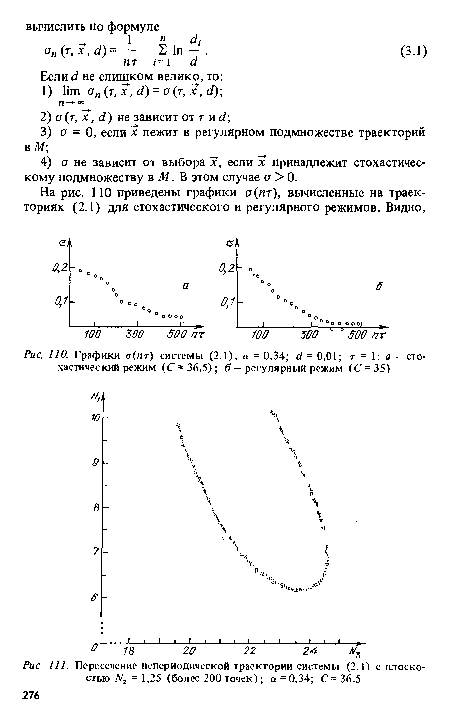
| Графики о (пт) системы (2.1), а = 0,34; <1 = 0,01; т = 1 |
 |
Далее
| Пересечение непериодической траектории системы (2.1) с плоскостью Ыг - 1,25 (более 200точек); а = 0,34; С= 36,5 |
 |
Далее
| График функции 5 (?) системы |
 |
Далее
| Области различных динамических режимов для системы (4.1) |
 |
Далее
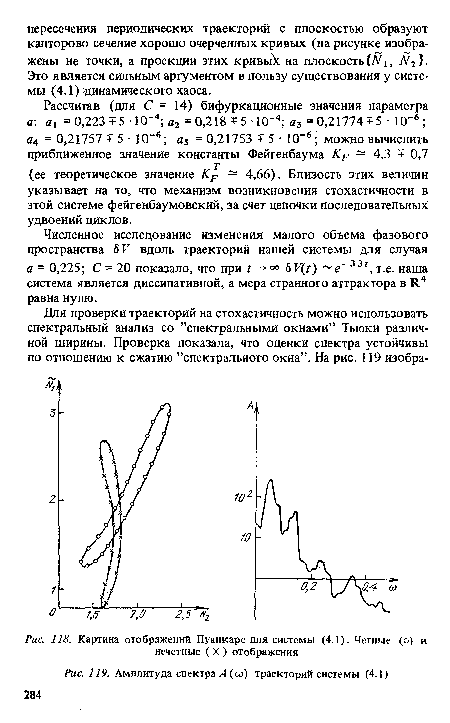
| Картина отображений Пуанкаре для системы (4.1). Четные (о) и нечетные ( X ) отображения |
 |
Далее
| Амплитуда спектра A(oj) траекторий системы (4.1) |
 |
Далее
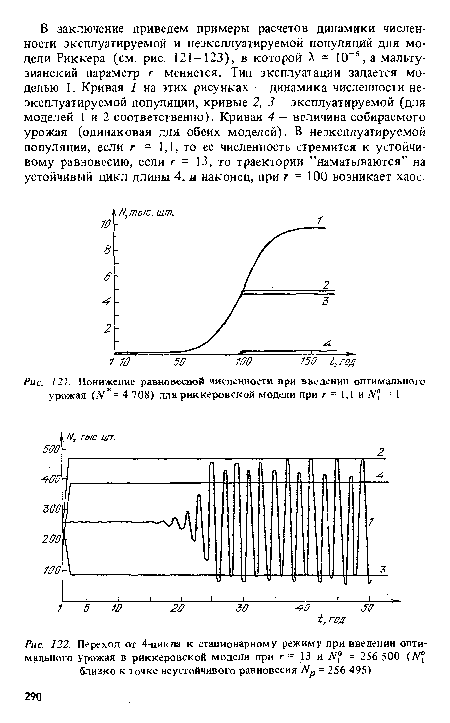
| Понижение равновесной численности при введении оптимального урожая (N - 4 708) для риккеровской модели при г = 1,1 и N° = 1 |
 |
Далее
| Переход от 4-цикла к стационарному режиму при введении оптимального урожая в риккеровской модели при г = 13 и N° = 256 500 (№1 близко к точке неустойчивого равновесия = 256 495) |
 |
Далее
| Ликвидация "хаоса” при введении оптимального урожая в рикке-ровской модели при г = 100 и N° = 460 516 (точка неустойчивого равновесия = 460 517) |
 |
Далее
| Зависимость численности серой цапли от времени |
 |
Далее
| Области различных типов динамики численности популяций вблизи нулевой границы (границы вырождения); / - популяция вырождается за конечное время; II - популяция вырождается за бесконечное время (имеет малую численность на большом интервале времени, т.е. ее численность за конечное время может стать ниже любого критического порога); III - популяция не вырождается |
 |
Далее
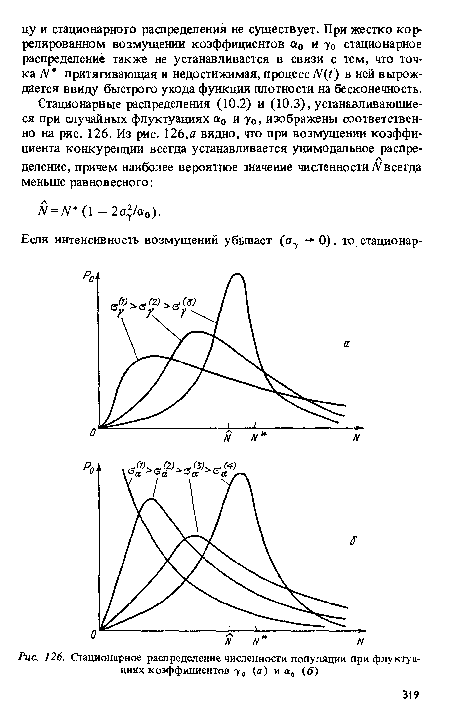
| Стационарное распределение численности популяции при флуктуациях коэффициентов у„ (а) и«, (б) |
 |
Далее
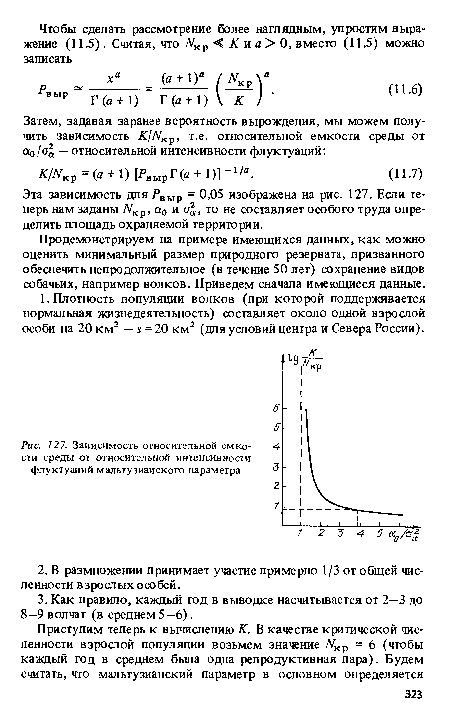
| Зависимость относительной емко- 4 сти среды от относительной интенсивности флуктуаций мальтузианского параметра & |
 |
Далее
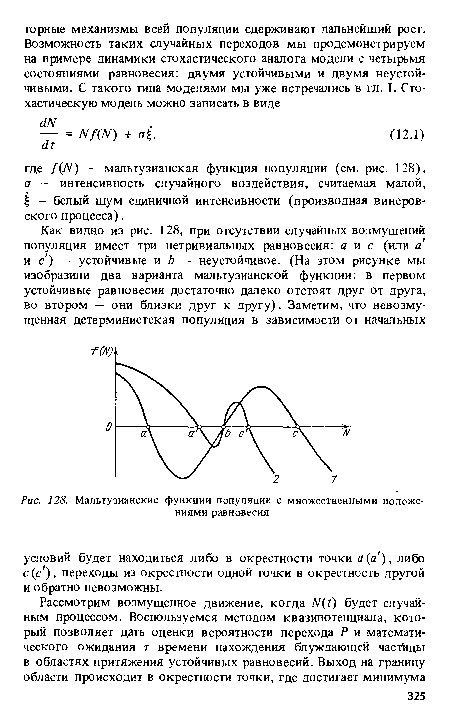
| Мальтузианские функции популяции с множественными положениями равновесия |
 |
Далее
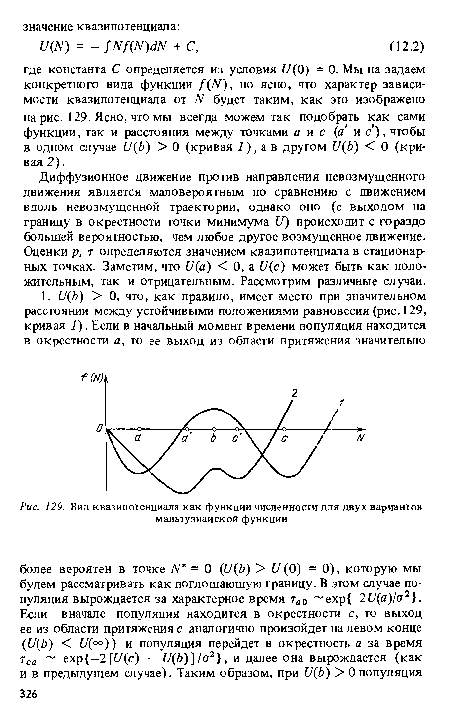
| Вид квазипотенциала как функции численности для двух вариантов мальтузианской функции |
 |
Далее
| Область различных типов динамики системы ’’хищник — жертва” |
 |
Далее
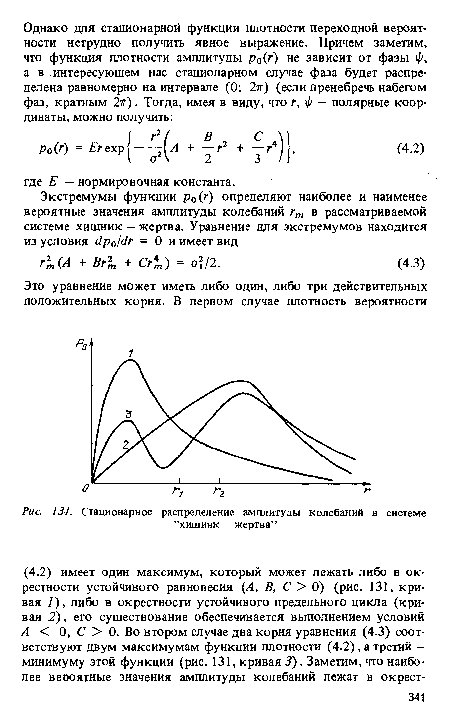
| Стационарное распределение амплитуды колебаний в системе |
 |
Далее
