Экология СПРАВОЧНИК

Ударная нагрузка измерялась де Холлером [35]. Большой пьезоэлектрический кристалл прикреплялся на лицевой поверхности образца, пересекающего вертикальную струю воды в роторной установке с вертикальной струей воды. При скорости 35 м/с среднее давление удара, которое определялось путем деления нагрузки на площадь поперечного сечения струи, оказалось равным 31 МПа. Расчетным путем была получена величина 48,5 МПа. Позднее Бичинг [11] предположил, что это расхождение могло быть вызвано текучестью поверхности твердого тела под датчиком. Более вероятная причина состоит в том, что эффективная площадь поверхности, подверженной сжатию, значительно меньше площади поперечного сечения струи.[ ...]

Измеренные значения скорости оказались в очень хорошем согласии с этим уравнением.[ ...]

Имеется довод в пользу того, что давление в центральной зоне сжатия постоянно и определяется уравнением (10). Этот довод состоит в том, что скорость частиц в зоне сжатия постоянна и равна скорости удара. Новым в работе [49] явилось предположение, что растекание из-под капли начинается не в момент удара. Показано также, что скорость волны является функцией состояния.[ ...]

Хэнкоке и Брайтон [70] попытались определить величину угла течения, т. е. угла, который составляет граница капли с поверхностью твердого тела в момент, когда начинается течение. Выполненные ими измерения дали значения угла течения 17° для скорости 50—150 м/с. Эти значения существенно превышают полученные по уравнению (18).[ ...]

Скорость струи относительно некоторой неподвижной точки на поверхности твердого тела определяется уравнением (15). Следует отметить, что давление на границе капли и скорость струп стремятся к бесконечности, когда угол натекания потока стремится к нулю. Уравнения (15) и (21) были выведены Биркгоф-фом и др. [14] при анализе разрушения металлических облицовок в профилированном заряде и Тейлором [155] при исследовании косого удара плоской струи в движущееся твердое тело.[ ...]

Другое подтверждение неравномерности пространственного распределения давления на нагрузочной стадии удара с повышением давления к границе контактной зоны до начала течения дают исследования удара жестких тел в плоскую поверхность жидкости. Скалак и Фейт [144] рассчитали распределение давления по поверхности тупого жесткого клина при ударе его о плоскую поверхность жидкости. Они получили особенность на границе в распределении давления, однако среднее давление на контактной поверхности оказалось равным давлению гидравлического удара.[ ...]

Угол между границами капли и поверхностью твердого тела в момент возникновения течения измерялся непосредственно по фотографиям, а также рассчитывался, исходя из ширины болны давления, которая распространяется через каплю. Была получена величина угла в пределах 10—20° при среднем значении 1Г в диапазоне скоростей 30—100 м/с. Эти значения существенно выше, чем рассчитанные по уравнению (18). В этом же диапазоне скоростей удара скорость бокового растекания приблизительно в 10 раз превышает скорость удара.[ ...]

Типичные результаты измерений показаны на рис. 9. Представленная кривая характеризует изменение максимального давления удара Р тах вдоль оси х под водяной каплей диаметром 5 мм при ударе в нее пули со скоростью 100 м/с. Распределение давления симметрично относительно центра удара. Максимумы давления наблюдаются на расстоянии 0,5 мм от центра удара с каждой стороны. Давление в центре составляет 110 МПа, а на краях 260 МПа. Если учесть деформацию датчика при ударе (т. е. рассчитать давление, которое было бы при ударе о жесткую поверхность), эти давления будут равны РоС0и и 2,5 роСоО соответственно.[ ...]

Сходные результаты были получены с бромбензолом (плотность которого в 1,5 раза выше плотности воды) и минеральным маслом (вязкость которого в 60 раз выше вязкости воды) при скорости удара 100 м/с. Аналогичные кривые получены и при других скоростях удара и диаметрах капли.[ ...]

Рисунки к данной главе:

Волны сжатия в капле воды диаметром 4 мм при ударе о твердую поверхность со скоростью

Удар капли со скоростью 60 м/с. Скорость растекания струи 560 м/с [28].

Распределение максимального напряжения при ударе водяной стругг диаметром 50 мм по нормали к поверхности плоского алюминиевого датчика давления со скоростью

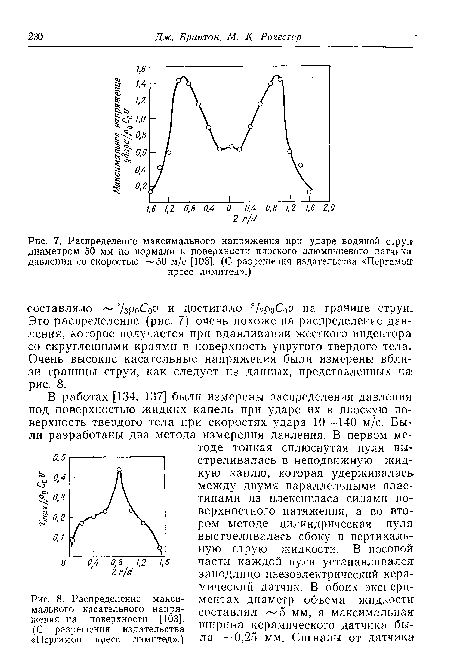Распределение максимального касательного напряжения на поверхности [103]. (С разрешения издательства «Пергамон пресс лимитед».)

Распределение максимального давления удара капли воды диаметром 5 мм при скорости 100 м/с [137]. (Собственность правительства Великобритании.)

Вернуться к оглавлению