Экология СПРАВОЧНИК

В разд. 3.1 кратко изложены результаты аналитических исследований, которые предложены в литературе для описания различных особенностей взаимодействия одиночной капли воды с твердой поверхностью при дозвуковых скоростях удара, а также общей реакции материала преграды на приложенную нагрузку. Важной задачей при исследовании эрозии почвы является определение характеристик растекания капли воды при ударе о плоскую поверхность твердого тела или слоя жидкости при скорости удара, не превышающей 10 м/с. Соответствующие данные по эрозии почвы, опубликованные в литературе, кратко изложены в разд. 3.3. Но они пока не содержат результатов непосредственных наблюдений и анализа механики уноса почвы при ударном воздействии капли воды.[ ...]

Все эти предположения различной степени общности будут рассмотрены ниже. В недавно опубликованном докладе Национальной совещательной комиссии по материалам [88] кратко изложено современное состояние вопроса, посвященного разработкам моделей численных расчетов на ЭВМ нестационарных пространственных распределений давления, возникающего при ударе и воздействующего на поверхность твердого тела. В то время как обзор численных результатов имеет довольно ограниченное применение, общие методы численного решения основных уравнений механики сплошной среды представляют интерес для разработчиков программ, в которых используются конечно-разностные методы. Конечно-разностные схемы вычислений позволяют рассчитать во времени процесс удара капли воды о поверхность твердого тела, а также определить для любого момента времени напряжения, возникающие в материале преграды.[ ...]

При определении эрозионной стойкости материалов обычно не учитывают особенностей процесса ударного воздействия жидкости, однако, чтобы разработать материалы с повышенной эрозионной стойкостью, необходимо прежде всего понять, каким образом возникает повреждение материала и происходит его последующее удаление. Как указывалось в разд. 2.3, задача исследования механизма эрозии материала заключается в определении того, каким образом жидкость после удара взаимодействует с характерными элементами исходной и поврежденной поверхности преграды. Для описания основных особенностей кинематики столкновения капли воды с гладкой плоской поверхностью необходимо использовать современные методы анализа и результаты экспериментальных наблюдений.[ ...]

Типичная картина деформации жидкой сферической частицы при ее ударе о поверхность схематично показана на рис. 2. Сложным оказался вопрос о том, в какой момент после удара капли начинается поперечное струйное растекание жидкости. Выдвинута гипотеза [33, 65], что поперечное растекание начинается вскоре после удара капли о поверхности, тогда как другие исследователи [19, 59, 89] придерживаются мнения, что для этого требуется выполнение условия равенства скорости расширения контактной области между каплей и плоской поверхностью преграды скорости распространения ударной волны в жидкости.[ ...]

В работе [19] выдвинуто предположение, что поперечное растекание жидкости начинается тогда, когда быстро убывающая ■скорость границы контактной области между каплей и поверхностью твердого тела становится равной скорости распространения фронта ударной волны в жидкости. До этого момента фронт ударной волны скользит по поверхности твердого тела. В результате сжатая жидкость ограничена жесткой поверхностью и фронтом ударной волны, который перемещается в невозмущенной жидкости. И только после того, как ударная волна обгонит границу расширяющейся контактной области, появляется свободная поверхность, через которую начинается поперечное растекание.[ ...]

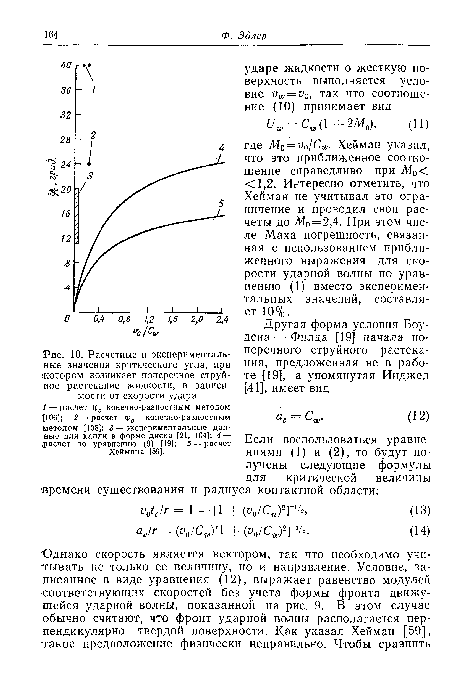
Поскольку первоначально скорость расширения контактной области превышает скорость распространения ударной волны в жидкости, граница области сжатия движется вдоль поверхности преграды быстрее, чем вдоль оси симметрии. В начальный период удара область сжатия имеет форму сплющенной полусферы (рис. 9). Критическое условие возникновения поперечного струйного растекания, предложенное Боуденом и Филдом [19], можно выразить с помощью уравнений (1) и (2), используя простые геометрические соотношения между векторами скоростей и смещений. Подробно условия поперечного растекания обсуждались в работах [41, 59].[ ...]

Это широкоизвестное соотношение выражает условие возникновения поперечного растекания жидкости. Хейман [59] указал, что при выводе соотношений в работе [19] фронт ударной волны в критической точке предполагался расположенным по нормали к поверхности капли, однако это не соответствует физической картине течения для тех конфигураций областей, которые возникают после удара.[ ...]

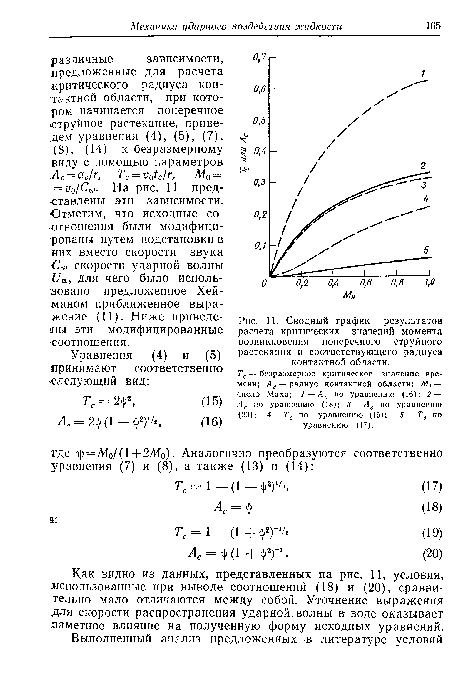
Тс — безразмерное критическое значение времени; Ас— радиус контактной области; М0 — число Маха; 1—Ас по уравнению (16); 2 — Ас по уравнению (18); 3 — АС по уравнению (20); 4 — Тс по уравнению (15); 5 — Тс по уравнению (17).[ ...]

Трудно сказать в настоящее время, связаны ли большие значения угла фс, при котором возникает понеречное растекание с накоплением погрешности при использовании конечного размера вычислительной сетки в программах численного расчета на что до некоторой степени указывает снижение величины ц>с с уменьшением шага сетки, или это связано с предположением о сжимаемости жидкости и с тем, что не учитываются другие гидродинамические эффекты, имеющие место после начальной фазы удара. Отметим, что если пренебречь влиянием вязкости то получают более низкие значения угла фс.[ ...]

Инджел [35] выполнила обширную программу экспериментальных и теоретических исследований, чтобы составить представление об отдельных стадиях разрушения капли воды диаметром 5,7 мм при ударе о поверхность стекла со скоростями, достигающими скорости свободного падения (8,2 м/с)- Инджел разработала метод фотографирования, который позволяет измерить радиус внешнего края струи жидкости, возникающей при разрушении капли. Она также теоретически получила выражение для зависимости от времени максимального радиуса этой области, соответствующим образом распределив начальную кинетическую энергию, которую имела капля непосредственно перед ударом о поверхность. Результаты экспериментальных наблюдений были схематизированы и использованы в теоретических расчетах. Оказалось, что скорость струи жидкости достигает величины, которая в 10 раз превышает скорость капли перед ударом.[ ...]

Рисунки к данной главе:

Геометрические характеристики области взаимодействия жидкой капли с жесткой плоской поверхностью.

Расчетные и экспериментальные значения критического угла, при ‘котором возникает поперечное струйное растекание жидкости, в зависимости от скорости удара.

Сводный график результатов расчета критических значений момента возникновения поперечного струйного растекания и соответствующего радиуса контактной области.

Распределение давления по поверхности раздела в момент достижения максимальных значений при ударном воздействии воды на жесткую поверхность (результаты частично воспроизводятся по данным работы [69]).

Распределение напряжений растяжения в преграде из известковонатриевого стекла при ударе капли воды диаметром 1,8 мм со скоростью

Геометрические параметры

Вернуться к оглавлению