Проблемы удара настолько сложны, что поле ударных напряжений может быть рассчитано с достаточной точностью только с помощью численных конечно-разностных методов. До настоящего времени выполнено немного подобных расчетов, поэтому еще трудно представить полную картину поля ударных напряжений. Однако эта задача может быть частично решена с помощью приближенных аналитических методов и имеющихся численных результатов.[ ...]
Описание напряжений при ударе удобно начать с анализа различных типов волн напряжений, возникающих при ударе, а затем перейти к динамическим напряжениям, используя ударную нагрузку или давление удара в качестве граничных условий.[ ...]
Аналогичная волновая картина будет наблюдаться при ударе. Особое значение имеют ослабление волны, связанное со сферическим расширением (которое приближенно описывается уравнениями (3) и (8)), и распад упругопластической ударной волны на упругую и упругопластическую волны в момент времени ¿ .[ ...]
Динамические напряжения, возникающие при ударе частицы в преграду, удобно рассматривать в два этапа: для начальной стадии контакта, для которой имеются приближенные аналитические решения для первоначально плоских поверхностей, а затем для глубокого проникания, основные закономерности которого можно описать с помощью решения для полости под давлением. Основной интерес для механики разрушения представляют напряжения растяжения, на которых в дальнейшем и будет сосредоточено внимание.[ ...]
Когда частица проникает на заметную глубину или скорость роста зоны контакта значительно отклоняется от зависимости. ¿4 роль больших динамических напряжений растяжения, связанных с волной Рэлея, уменьшается и преобладающее влияние начинают играть напряжения растяжения в глубине тела. Такое поведение следует из решения, полученного Цаем [47] для абсолютно упругого удара. Его расчеты радиальных поверхностных напряжений показали, что их величина соответствует решению Герца для квазистатического случая (о, =(1—2у)р(а/г)2) при максимальной глубине проникания. Это подтверждается результатами численных расчетов для абсолютно упругого удара (рис. 31) и упругопластического удара жесткой частицы (рис. 32). Таким образом, решение Блоуэрса имеет ограниченное (но тем не менее важное) применение к удару твердых частиц.[ ...]
Рис, 32. Напряжения, возникающие при ударе жесткой частицы диаметром 400 мкм в преграду из 2пЭ [16]. о — растягивающие напряжения в плоскости при внедрении (ир = 860 м/с); б— растягивающие напряжения вне плоскости при внедрении (ур=860 м/с); в — растягивающие напряжения в плоскости при разгрузке (о„=200 м/с).[ ...]
Рисунки к данной главе:
| Диаграммы время — расстояние для полости, подвергающейся динамическому воздействию давления. |
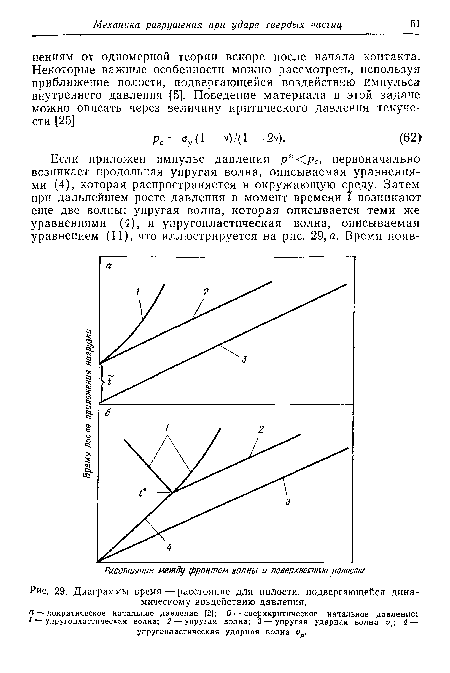 |
| Профили напряжений, полученные из решения Блоуэрса |
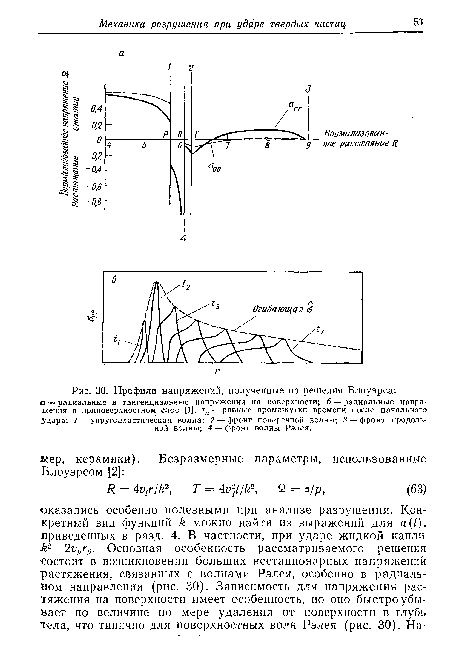 |
![Напряжения, возникающие при абсолютно упругом ударе и при эквивалентном внедрении под действием квазистатической нагрузки [41]. •а — растягивающие напряжения в плоскости; 6 — растягивающие напряжения вне плоскости.](/static/pngsmall/950005014.png)