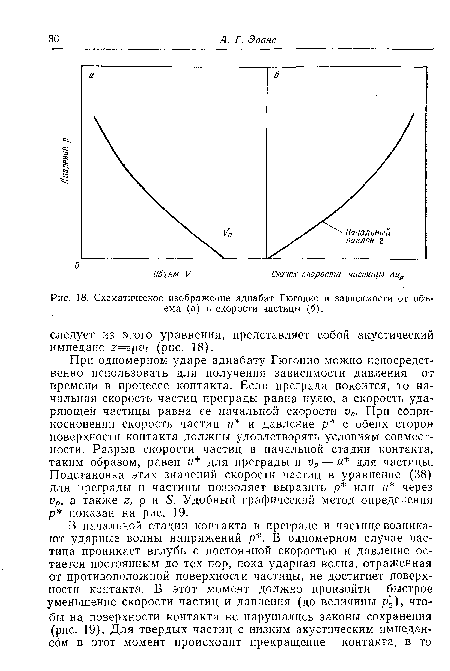
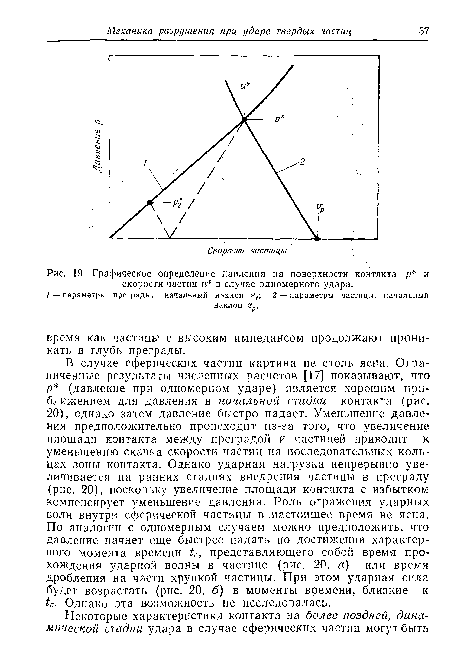
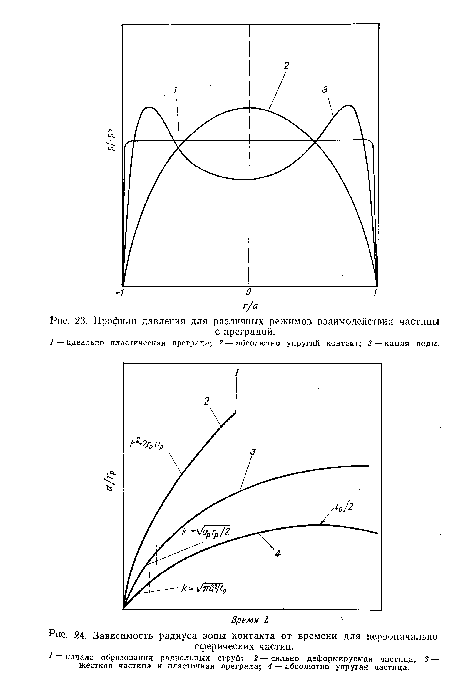
При одномерном ударе адиабату Гюгонио можно непосредственно использовать для получения зависимости давления от времени в процессе контакта. Если преграда покоится, то начальная скорость частиц преграды равна нулю, а скорость ударяющей частицы равна ее начальной скорости ур. При соприкосновении скорость частиц и и давление р с обеих сторон поверхности контакта должны удовлетворять условиям совместности. Разрыв скорости частиц в начальной стадии контакта, таким образом, равен и для преграды и юр — и для частицы. Подстановка этих значений скорости частиц в уравнение (38) для преграды и частицы позволяет выразить р или и через ир, а также г, р и 5. Удобный графический метод определения р показан на рис. 19.[ ...]
Однако для этого случая можно получить только максимально возможную глубину внедрения (или силу), приравняв работу начальной кинетической энергии частицы. Оба эти решения не учитывают разгрузочных эффектов, связанных с отражением ударных волн в частице, и поэтому дают только верхнюю границу глубины внедрения. Некоторые важные параметры контакта (такие, как акустический импеданс, трещиностойкость, напряжение пластического течения) также не рассматривались при получении этих решений- Это ограничение, по-видимому, допустимое в случае глубокого внедрения, в случае неглубокого внедрения является достаточно серьезным.[ ...]
И наконец, следует ясно представлять, что все аналитические решения задачи о внедрении частицы в преграду имеют ряд существенных недостатков. Работа, затрачиваемая на пластическую деформацию материала при внедрении частицы, приводит к повышению температуры материала вблизи зоны пластической деформации. Это повышение температуры может существенно изменить поле напряжений, особенно на последних этапах внедрения, когда скорости деформации весьма умеренные. Величина этого эффекта зависит от свойств материала и количества движения частицы. Например, он будет, по-видимому, более заметным в керамических материалах, для которых работа пластической деформации на единицу объема велика (из-за большой величины напряжения пластического течения), отвод теплопроводностью из зоны пластических деформаций мал (из-за низкой теплопроводности) и напряжение пластического течения сильно зависит от температуры и скорости деформации. Следовательно, в некоторых случаях необходимо определять глубину внедрения с учетом удельной теплоемкости, теплопроводности и зависимости напряжения пластического течения от скорости деформации и температуры, роэтому необходимо создание приближенных аналитических моделей, которые позволят проводить предварительную оценку условий, при которых теплофизические свойства преграды, играют существенную роль. Зависимость пластического течения от скорости деформации также сказывается на изменении параметров контакта в процессе удара, поскольку скорость дефЬрмации в области, примыкающей к частице, изменяется на несколько порядков величины в промежуток времени от начала контакта до прекращения внедрения. Качественно зависимость от скорости приведет к некоторому увеличению давления и силы на ранних этапах контактирования и тем самым к смещению максимума ударной нагрузки в сторону меньших времен крнтакта.[ ...]
Рисунки к данной главе:
Вернуться к оглавлению