Сильная зависимость от длины волны указывает на важную роль гармонического анализа поверхностных волн, возникающих при ударе. Амплитуды волн различной частоты могут быть измерены экспериментально с помощью пьезоэлектрических датчиков (при акустических колебаниях) или получены расчетным яутем для простых случаев (например, для упругого удара).[ ...]
Амплитуда поверхностных волн быстро уменьшается с уменьшением длины волны [40], так что они имеют заметную величину лишь при частотах не более 100 кГц.[ ...]
Важное значение может иметь также отражение упругих волн от границ или поверхностей раздела. Наиболее просто это-явление можно проиллюстрировать на примере продольной волны, падающей на свободную поверхность. Сравнительно просто показать [32], исходя из условия равенства нулю нормального напряжения на свободной поверхности, что для продольной волны угол отражения равен углу падения, а амплитуда отраженной волны по величине равна амплитуде падающей волны, но противоположна по знаку (т. е. падающая волка сжатия отражается как волна растяжения); это особенно-важно для разрушения сколом. Из условия отсутствия касательных напряжений на свободной поверхности следует, что при отражении продольной падающей волны может возникать поперечная волна (за исключением случая падения по нормали), при котором угол и амплитуда отраженной волны связаны с соответствующими параметрами падающей волны отношением: скоростей продольной и поперечной волн [32].[ ...]
Поведение материала при больших скоростях пластической-деформации оказывается значительно более сложным, чем в случае упругой деформации, главным образом из-за влияния? скорости деформации, упрочнения и давления на касательное напряжение пластического течения. Ниже вкратце рассматриваются некоторые явления, играющие важную роль при ударе.[ ...]
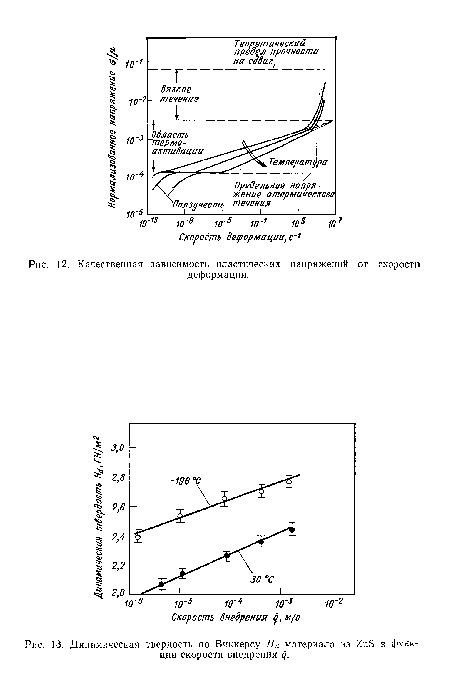
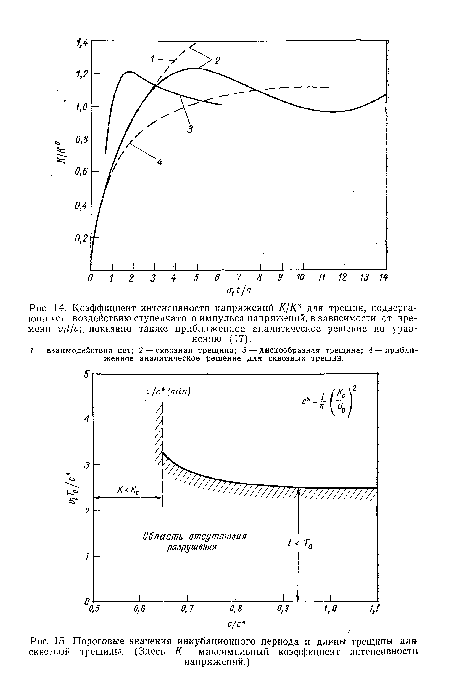
Влияние скорости деформации на пластическое течение также имеет важное значение для расчета и анализа процесса разрушения при ударе. На рис. 12 показана типичная зависимость пластических напряжений от скорости деформации [37]. Для задач об ударном воздействии большой интерес представляют режимы термоактивации и вязкого течения. В режиме термоактивации (рис. 13) скорость деформации весьма чувствительна к механизму взаимодействия дислокаций [31]. Кроме того, размер области, соответствующий этому режиму, зависит от свойств материала через доминирующие процессы взаимодействия дислокаций. При больших скоростях деформации происходит переход к режиму вязкого течения. Характер кривой в этом случае объясняется высокой скоростью движения дислокаций [6, 21, 49]. Подробные данные имеются только для весьма небольшого числа материалов, представляющих интерес. Однако при анализе экспериментальных данных по ударному воздействию необходимо учитывать возможность существования режима вязкого течения при больших скоростях деформации, как это будет показано в последующих разделах.[ ...]
Настоящий анализ можно обобщить на импульсы произвольной формы путем суперпозиции большого числа прямоугольных импульсов напряжения Аа, соответствующих бесконечно малым интервалам времени Аt. Получим аналитическое выражение, используя формулу (17) для КО); точный результат можно найти численно. Коэффициент интенсивности напряжений в момент времени to равен сумме коэффициентов интенсивности в момент ¿о от каждого интервала А1, т. е.[ ...]
Подобный анализ можно провести для случая наклонного-падения импульса напряжения [20]. Основные выводы, касающиеся существования инкубационного периода и его зависимости от длины трещины и профиля напряжения сохраняют свою силу, однако в деталях имеются некоторые различия.[ ...]
Как и выше, соотношение (31) следует рассматривать как некий постулат, пока не будут получены подтверждающие или опровергающие его данные.[ ...]
Аналогичные результаты можно получить из формулы (31) для трещин конечной длины и импульсов произвольной формы.[ ...]
В приведенном выше анализе не учитывалось ветвление трещины, имеющее место при некоторой скорости распространения трещины, соизмеримой со скоростью волны Рэлея (см. [30]). Поскольку ветвление трещин не часто наблюдалось в представляющих здесь интерес условиях удара (разд. 2), пренебрежение этим явлением, по-видимому, оправданно. Однако имеется много других случаев, в которых необходимо учитывать ветвление трещин путем модификации условия роста трещины (уравнение (24)).[ ...]
Рисунки к данной главе:
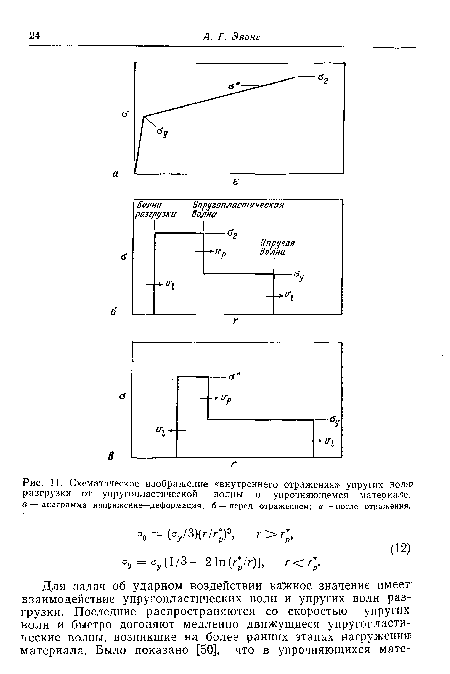
| Размеры радиальных и поперечных трещин в преграде из 2пБ для квазистатического и динамического условий проникания. |
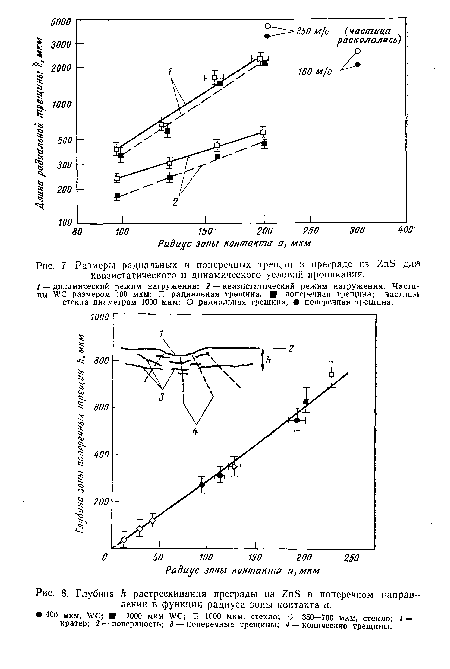 |
| Глубина h растрескивания преграды из ZnS в поперечном направлении в функции радиуса зоны контакта а. |
 |
| Упругие напряжения сдвига, возникающие в сферической полости фадиусом г0 под действием ступенчатого импульса давления; показаны так- |
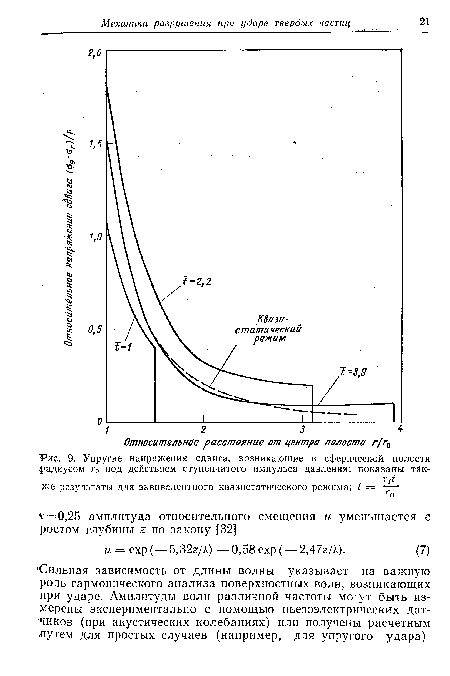 |
| Тангенциальные напряжения, возникающие в полости, подвергаемой воздействию сверхкритического (упругопластического) импульса давления; показаны результаты для эквивалентного квазистатического режима. |
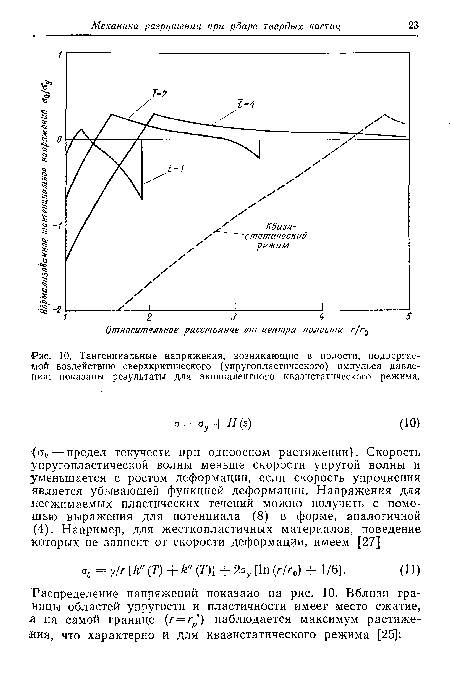 |
| Качественная зависимость пластических напряжений от скорости |
 |
| Динамическая твердость по Виккерсу На материала из 2пБ в функции скорости внедрения д. |
 |
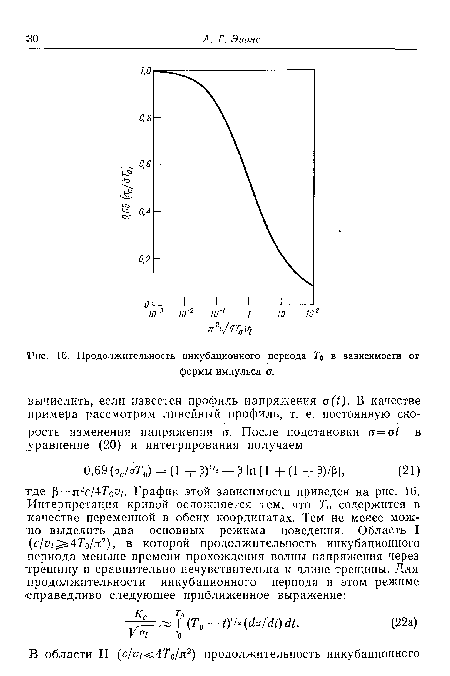
| Пороговые значения инкубационного периода и длины трещины дл» сквозной трещины. (Здесь К — максимальный коэффициент интенсивности |
 |
| Продолжительность инкубационного периода То в зависимости от |
 |
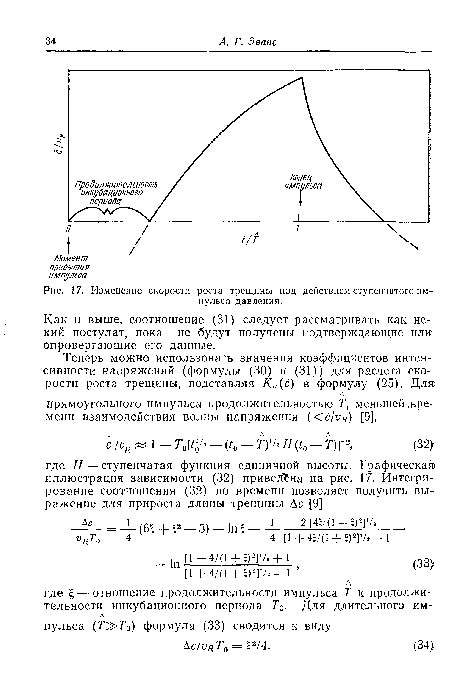
| Изменение скорости роста трещины под действием ступенчатого импульса давления. |
 |