Экология СПРАВОЧНИК

При небольших объемных модулях (обычно имеющих место в случае 1) гидравлическое воздействие, оказываемое втекающим потоком, по-видимому, должно быть пренебрежимо мало. В остальных случаях поступающая вода скорее всего способна взаимодействовать с водными массами озера, вызывая по крайней мере локальное турбулентное перемешивание/вовлечение. Эти процессы будут предметом нашего обсуждения, приводимого ниже.[ ...]

Толщина слоя по механизму вовлечения (основных вод) увеличивается по мере проникновения речного притока в водохранилище. Соответствующее увеличение объема потока АС может быть вычислено по формуле, также предложенной Имбергером и др.[ ...]

Если определена глубина залегания равновесного уровня, то могут быть установлены как толщина приточного слоя, так и распределение в зоне впадения приточных вод между модельными подслоями (см. также п. 7.2).[ ...]

На первых порах исследования по определению траектории потока, равновесного уровня (высоты) и характера смешения таких притоков, обладающих плавучестью, фокусировались, так сказать, на подмножествах этой проблемы. Например, избирались струи, в поведении которых доминирующим фактором является количество движения [72]. В других работах рассматривались случаи идеально горизонтальной или идеально вертикальной струи с быстрыми переходами между этими состояниями.[ ...]

В действительности траектория струи представляет собой кривую линию (см. рис. 4.7) и в многочисленных попытках (см., например, [69, 217, 228, 236, 295]) смоделировать струи, обладающие плавучестью, использовалась криволинейная система координат. Квази-коническая конфигурация струй обусловлена тем, что поток поступает в водохранилище из круглого отверстия (называемого точечным или трехмерным источником). Часто случается, однако, что поступление воды в водоем осуществляется через линейку диффузоров или прямоугольные отверстия типа «щели». В такой ситуации образуется линейный или двухмерный шлейф, траектория движения которого не идентична конфигурации пути распространения струи трехмерного источника (несмотря на сходство теоретических описаний, стоящих за каждым из этих случаев).[ ...]

Если установлены координаты ( , г) конца ZFE и «начальные» характеристики потока, то разнообразные интегральные модели используют эти данные, как если бы они относились к источнику, перенесенному в точку (хи z ).[ ...]

Интегральные модели основываются на решении системы проинтегрированных по вертикальному сечению шлейфа дифференциальных уравнений, выражающих законы сохранения. Соответствующие потоки характеризуются значениями их аксиальных скоростей. Этот подход был впервые предложен Мортоном и др. [363], а полный вывод уравнений появился позднее в работе Мортона за 1971 г. [362]. Анализ свидетельствует о том, что одно из этих уравнений избыточно. В моделях разнообразным образом используется уравнение сохранения кинетической энергии вместо уравнения плавучести (или наоборот). Уравнения количества движения могут быть записаны либо для радиальной и аксиальной, либо для вертикальной и горизонтальной составляющих.[ ...]

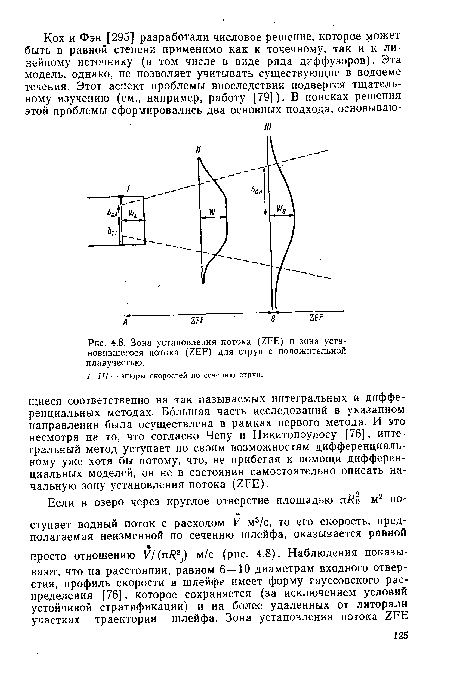
Ф — угол относительно горизонтальной плоскости, а индекс 0 относится к исходным величинам.[ ...]

Заметим в скобках, что в работах, использующих уравнения рассматриваемого круга, можно встретить несогласованность в применяемых обозначениях. Действительно, в статье Райта и др.[ ...]

Таким образом, отношение /м /« в действительности не что иное, как денсиметрическое число Фруда (уравнение (4.38)). Приведенный подход оказался полезным при анализе линейных источников (погруженные выводные коллекторы) (см., например, [609, 610]). При выполнении такого анализа масштабы длин должны быть определены заново для линейного источника (сравни уравнения (4.55) — (4.57) для точечного источника). Робертс и Маттюс [448] применили этот метод к измерению распространения притоков с очень слабой плавучестью в линейно стратифицированном водоеме. Согласно полученным ими выводам, ширина струи и расстояние до ее полного смешения с окружающей водной средой могут быть прямо связаны с указанными масштабами длин. Более подробный анализ результатов этого имитационного моделирования приводится в работе Робертса и Маттюса [449].[ ...]

Рисунки к данной главе:

Три характерных положения втекающего потока

Траектория и характеристики смешения погруженных струй с положительной плавучестью.

Зона установления потока (ZFE) и зона установившегося потока (ZEF) для струи с положительной плавучестью.

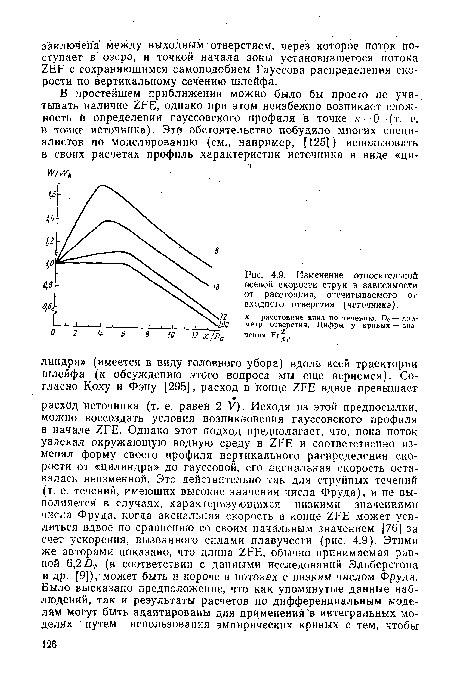
Изменение относительной осевой скорости струи в зависимости от расстояния, отсчитываемого от входного отверстия (источника).

Конфигурации погруженное и приповерхностной струй с положительной плавучестью [204].