Экология СПРАВОЧНИК

В этой главе обсуждается гидродинамика озер. Течения в них возникают под воздействием ветров (п. 4.1), но могут быть обусловлены также притоками и стоками (п. 4.2). С позиций управления качеством воды наиболее важный аспект, связанный с притоками и стоками, заключается в проблеме локализации входа в озеро и выхода из него, соответственно, приточных и сточных вод. В случае любого из этих типов течений вертикальные распределения лимнологических параметров в наиболее существенной степени определяются вертикальными профилями скорости потока (т. е. сдвигом потока, см. п. 4.3). Следующими по значению факторами в этом плане являются ветровое волнение и сейши (п. 4.4), которые временами могут даже доминировать над ветровым турбулентным перемешиванием. Наконец, в п. 4.5 обсуждаются некоторые аспекты горизонтальной диффузии загрязняющих компонентов.[ ...]

Система уравнений, приведенная выше, может быть аналитически решена, если известны граничные условия. Основное затруднение здесь состоит в том, что нормальная компонента скорости должна исчезать на любой твердой поверхности. Если учесть силы трения о боковые стенки, то эта система уравнений может быть применена и для вычисления меридиональной компоненты скорости.[ ...]

Первоначально рассмотрение задачи ограничивалось случаями идеализированных форм чаши озера: круглой [40] и прямоугольной [320, 321]. Применение мощных вычислительных машин позволило осуществить имитационные расчеты для озер более разнообразных форм: см., например, работы Мёти и Рэо [370] и Саймонса [482, 483] соответственно по озерам Мичиган и Онтарио.[ ...]

В принципе, можно приступать к решению приведенной выше системы уравнений, если известны или оценены напряжения И, В, например, в случае упрощенных ситуаций, когда В = 0, или же = 11, V)]. Необходимые граничные условия задаются в терминах переноса в виде «нулевых переносов, перпендикулярных береговой черте».[ ...]

Ксенеди [92] отмечает, что эти уравнения оказываются согласованными, если дН/ду = 0. Таким образом, результирующий перенос всегда осуществляется вдоль изобат (т. е. линий постоянной глубины).[ ...]

В северном полушарии это соответствует переносу (вдоль оси х) вправо от направления ветра. Получить локальное решение менее просто, и этот вопрос подробно обсуждается в п. 4.3.[ ...]

Усредненные пространственные структуры циркуляций для оз. Онтарио приведены в работах Пикетта [411, 412]. Полученные на основе расчетов по модели Рэо и Мёти [425], они обнаруживают хорошее соответствие с реалиями при удачном выборе значения коэффициента донного трения. Подобные расчеты были выполнены для оз. Эри Гедни и Ликом [181], а также Бонемом-Картером и Томасом [52] для оз. Онтарио.[ ...]

Слева — вид сверху, справа — вид сбоку, 1 -ница раздела.[ ...]

Слева — на поверхности бассейна; справа — на расстоянии 0,16 м над границей раздела слоев.[ ...]

Эта пара уравнений описывает инерционные реакции (т. е. инерционные течения) озера. Движение носит периодический характер с периодом 2л/ ( 17 ч для средних широт). Хотя этот тип движения редко наблюдается сам по себе в озерах с размерами менее 10 км, тем не менее он лежит в основе всей озерной гидродинамики.[ ...]

Рисунки к данной главе:

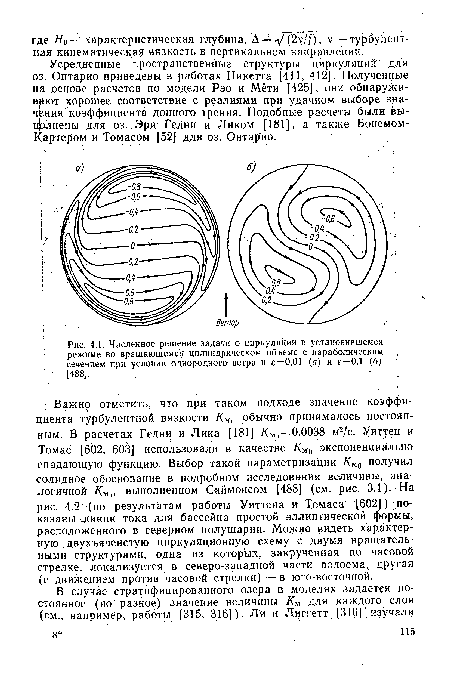
Численное решение задачи о циркуляции в установившемся режиме во вращающемся цилиндрическом объеме с параболическим сечением при условии однородного ветра и е=0,01 (а) и е=0,1 (б)

Поля функции тока в эллиптическом бассейне для трех случаев [602].

Характерный вертикальный профиль продольной составляющей потока в нестратифициро ванном озере.