Во всех предшествующих работах рассматривались стационарные модели осевых зон СОХ. Предположение о стационарном режиме формирования осевой магматической камеры (ОМК) позволило рассмотреть сложные интегральные модели эволюции осевых зон, включавшие процессы сегрегации и миграции расплава к осевой зоне, образования коры и формирования рельефа дна. Это ограничение можно считать оправданным, так как оценки показывают, что даже эпизодические внедрения магмы в осевой зоне могут создать квазистационарное термическое состояние области за исключением, вероятно, района интрузий шириной 50-500 м в самой близкой окрестности оси [288].[ ...]
Динамика формирования термического режима осевой зоны, включая образование корового очага магмы, также представляет большой интерес. Этому вопросу посвящены модели формирования корового очага магмы, представленные в работах [22, 23, 25, 26]. В указанных работах основное внимание было уделено анализу перехода дискретного поля температур, формируемого эпизодическими повторяющимися внедрениями осевых интрузий (шириной 5-50 м раз в 100-10 000 лет) в квазистационарное температурное поле осевой зоны центра спрединга.[ ...]
Как отмечалось, геолого-геофизические данные позволяют считать, что развитие осевых внутрико-ровых очагов магмы (стационарных, как в средне-и быстро раздвигающихся хребтах, или эпизодических, как в медленно раздвигающихся) проходит в присутствии относительно устойчивого широкого поднятия кровли астеносферы (см. рис. 3.7). Длительное существование такого поднятия при эпизодическом характере внедрений интрузий дает возможность построения сравнительно простой термической модели для численного анализа процесса формирования осевых коровых очагов магмы.[ ...]
В используемой в модели разностной схеме аппроксимации уравнения теплопроводности шаги Ах и Аг увеличивались в геометрической прогрессии от минимальных значений при х = 0 и г = 0, до максимальных при х=ХМ, 2 = ¿М. Минимальный шаг по координатам х и г определялся полушириной интрузии. Поэтому, например, для внедрения интрузии шириной 50 м раз в 1000 лет (средняя полу-скорость спрединга 5 см/год) минимальный шаг по времени, определяемый условием сохранения устойчивости решения и оцениваемый как Д/ = Ах /%, составлял 75 лет для нормальной теплопроводности коры (0,006 кал/см-с- °С) и 50 и 25 лет для “гидротермальных” значений теплопроводности коры, увеличенных, соответственно в 1,5 и в 3 раза по сравнению с нормальными.[ ...]
При описании спрединга с той же скоростью и внедрением интрузий шириной 5 м раз в 100 лет (хтш = 5 м) минимальные шаги по времени / должны быть уменьшены примерно в 100 раз. В промежутках между внедрениями, в периоды релаксации теплового режима, шаг по времени мог быть увеличен в 1,5-3 раза по сравнению с минимальным, но лишь по прошествии 10-20 шагов после внедрения интрузии.[ ...]
К существенным элементам модели относится приближенная трактовка процесса гидротермального теплообмена в породах коры приосевой области зон спрединга. Теплообмен в области активной деятельности гидротерм (зона неовулканизма и прилегающая к ней область трещиноватости) описывался введением эффективного коэффициента теплопроводности для пород коры данного блока. Этот коэффициент превосходил нормальную теплопроводность пород настолько, чтобы в рассматриваемом блоке коры воспроизводился градиент температуры, близкий к среднему значению, наблюдаемому в реальном блоке с гидротермальной активностью.[ ...]
Приближение эффективной теплопроводности оправдано еще и тем, что, как показали недавние исследования, гидротермосистемы осевых зон спрединга являются чрезвычайно сложными многоярусными и многофазовыми системами, в то время как основная информация об их деятельности, заключенная в распределении теплового потока на поверхности дна океана, носит как раз интегральный характер. Конкретный вид изменения эффективной теплопроводности с глубиной и расстоянием от оси спрединга, а также от времени процесса, существенно влияет на формирование очага. Поэтому обсуждение результатов моделирования мы начнем именно с этого вопроса.[ ...]
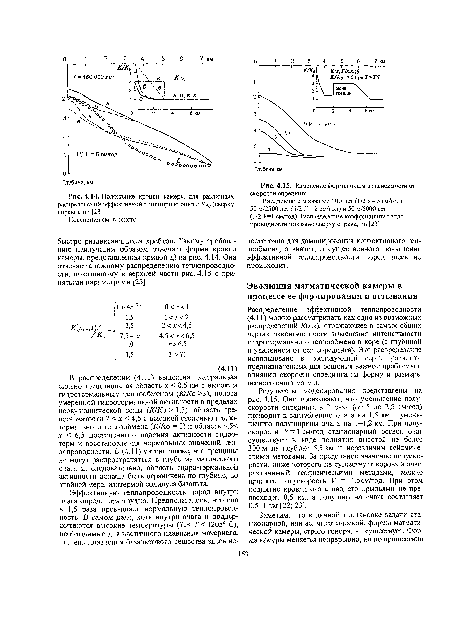
Естественно ожидать, что увеличение эффективной теплопроводности пород приведет к увеличению теплопотерь корового слоя и, как следствие, к заглублению кровли очага. Специальные расчеты, проведенные в рамках упрощенной модели с однородной теплопроводностью пород коры, подтвердили это. В примере с полускоростью спрединга 5 см/год (интрузия х = 5 м один раз в 100 лет) на оси для нормальных значений теплопроводности пород коры (К= 0,006 кал/см-с °С) кровля очага после 13 тыс. лет с начала внедрений располагалась на глубине около 1 км, тогда как для К = 0,06 кал/см-с-°С - на глубине 4,8 км по прошествии того же интервала времени. Это подтверждается и расчетами с переменными значениями теплопроводности (рис. 4.14).[ ...]
В распределении (4.11) выделена центральная сильно трещиноватая область х < 0,5 км с высоким гидротермальным теплообменом (К/Ко >3), полоса умеренной гидротермальной активности в пределах неовулканической зоны (К/Ко > 1,5), область трещиноватости 2 < х < 4,5 с высокой степенью гидротермального теплообмена (К/Ко = 3) и область 4,5< х < 6,5 постепенного падения активности гидротерм и восстановления нормальных значений теплопроводности. В (4.11) учтено также, что трещины не могут распространяться в глубь магматического очага и, следовательно, область гидро-термальной активности должна быть ограничена по глубине, по крайней мере, изотермой солидуса базальта.[ ...]
Рисунки к данной главе:
| Положение кровли камеры для различных распределений эффективной теплопроводности К(х) (сверху справа), по [23] |
![Положение кровли камеры для различных распределений эффективной теплопроводности К(х) (сверху справа), по [23]](/static/pngsmall/820745230.png) |
| Изменение формы очага в зависимости от скорости спрединга |
 |
Аналогичные главы в дргуих документах:
| См. далее:Описание модели |