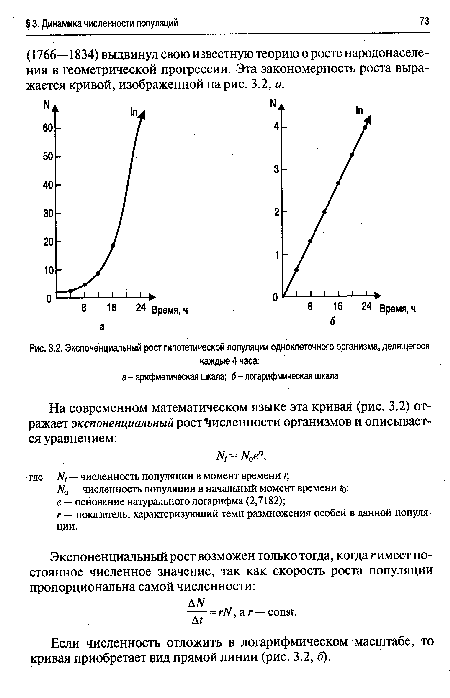
Если численность отложить в логарифмическом масштабе, то кривая приобретает вид прямой линии (рис. 3.2, б).[ ...]
Условия, сохраняющиеся длительное время постоянными, невозможны в природе. Если бы это было не так, то, например, обычные бактерии могли бы дать такую массу органического вещества, которая могла бы покрыть весь земной шар слоем толщиной в два метра за два часа.[ ...]
Однако такого в природе не происходит, так как существует множество ограничивающих факторов. Но есть примеры, когда при замедлении роста, т. е. при снижении г, экспоненциальный рост сохраняется, может он возникать и на коротких отрезках жизни популяций.[ ...]
Д. — чистая скорость воспроизводства, показывающая также, сколько вновь родившихся особей приходится на одну особь поколения родителей.[ ...]
Если Во = 1, то популяция стационарная, — численность ее сохраняется постоянной.[ ...]
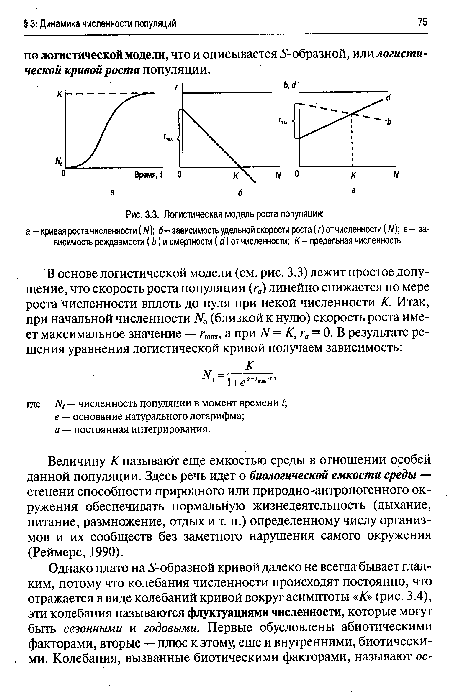
Воздействие экологических факторов на скорость роста популяции может довести численность популяции до стабильной (г = 0), либо ее уменьшить, т. е. экспоненциальный рост замедляется или останавливается полностью и 1-о6разная кривая экспоненциального роста как бы останавливается и выполаживается, превращаясь в так называемую Б-образную кривую (рис. 3.3, а).[ ...]
Величину К называют еще емкостью среды в отношении особей данной популяции. Здесь речь идет о биологической емкости среды — степени способности природного или природно-антропогенного окружения обеспечивать нормальную жизнедеятельность (дыхание, питание, размножение, отдых и т. п.) определенному числу организмов и их сообществ без заметного нарушения самого окружения (Реймерс, 1990).[ ...]
Рисунки к данной главе:
| Экспоненциальный рост гипотетической популяции одноклеточного организма, делящегося |
 |
| Логистическая модель роста популяции |
 |
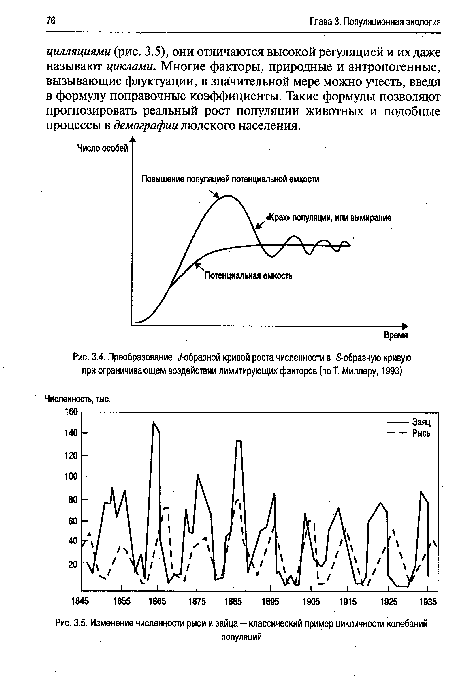
| Преобразование ^-образной кривой роста численности в 5-образную кривую при ограничивающем воздействии лимитирующих факторов (по Т. Миллеру, 1993) |
 |
| Изменение численности рыси и зайца - классический пример цикличности колебаний |
 |