Экология СПРАВОЧНИК

Оно и представляет собой математическую модель процесса изменения биомассы популяций. В экологической литературе уравнение (9.2) часто называют логистическим.[ ...]

Если теперь поставить вопрос о том, какова же будет биомасса в момент времени Т, то на него можно ответить экспериментально — дождаться этого момента и определить биомассу непосредственным измерением (вообще говоря, такое измерение может быть физически неосуществимым).[ ...]

Мы рассмотрели весьма упрощенную ситуацию, так как предполагали, что популяция не взаимодействует ни с какими другими популяциями, учет же этого обстоятельства, конечно, значительно усложняет модель.[ ...]

Рассмотрим одну из таких моделей. Будем обозначать биомассы двух популяций через х и у соответственно. Предположим, что обе популяции потребляют один и тот же корм, количество которого ограничено, и из-за этого находятся в конкурентной борьбе друг с другом.[ ...]

Первые члены правых частей системы (9.10) характеризуют скорость роста популяций при отсутствии ограничивающих факторов. Вторые члены учитывают те изменения в скоростях, которце вызываются ограниченностью корма.[ ...]

Задавая различные значения параметров, с помощью системы (9.10) можно описать взаимодействие двух популяций, одна из которых — хищник, а другая — жертва [36]. В литературе [47] более подробно описаны математические аспекты исследования системы (9.10).[ ...]

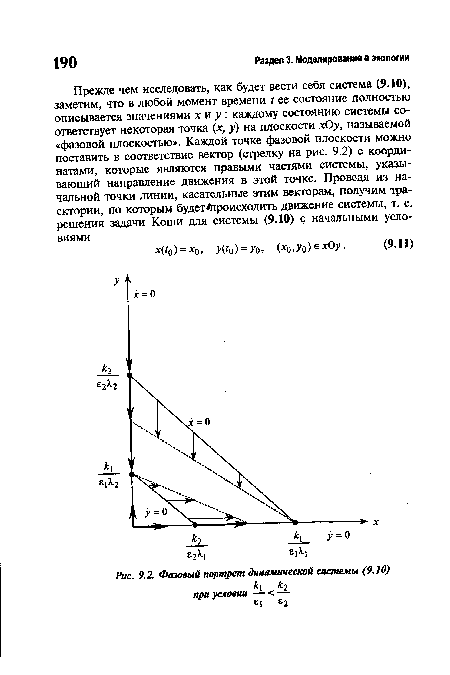
Чтобы составить представление о траекториях движения системы, построим линии, на которых х = 0 (здесь векторы параллельны оси Оу) и 1 = 0 (здесь векторы параллельны оси Ох).[ ...]

Рисунки к данной главе:

Зависимость биомассы от времени для различных значений параметров к, а и Хо

Фазовый портрет динамической системы (9.10)

Фазовый портрет динамической системы (9.10)

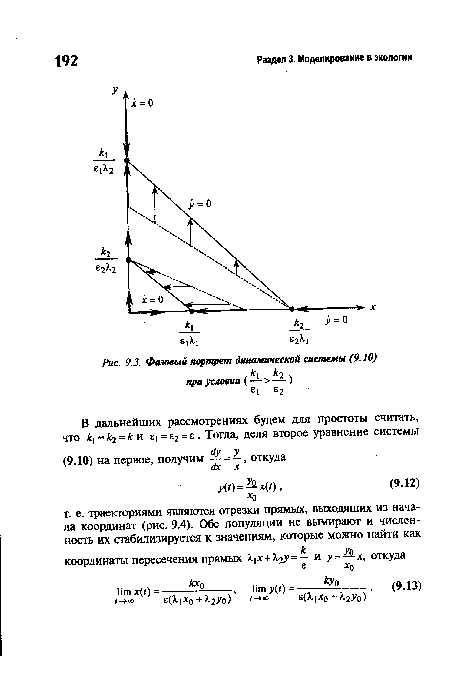Фазовый портрет динамической системы (9.10) при условиях ку = к2 = к , Е] =83 =е

Аналогичные главы в дргуих документах:

См. далее:Динамика популяций

См. далее:Динамика популяций

Вернуться к оглавлению