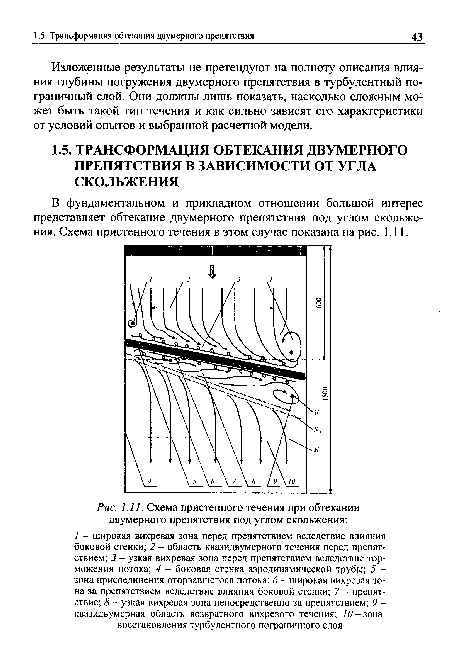
В фундаментальном и прикладном отношении большой интерес представляет обтекание двумерного препятствия под углом скольжения. Схема пристенного течения в этом случае показана на рис. 1.11.[ ...]
Глава 1. ИССЛЕДОВАНИЕ ТУРБУЛЕНТНОГО ТЕЧЕНИЯ.[ ...]
Как известно [Качанов Ю. С., 2000], в таких течениях направление вектора средней скорости зависит от расстояния до обтекаемой поверхности и вследствие возникновения поперечного градиента давления происходит сильное искривление линий тока, в результате чего вблизи подстилающей поверхности образуется так называемое поперечное, или вторичное, течение. Характер обтекания любых тел под углом скольжения всегда трехмерный.[ ...]
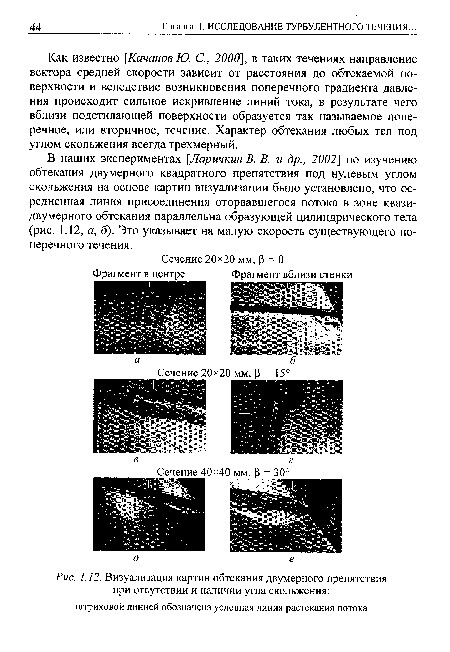
В наших экспериментах [Ларичкин В. В. и др., 2002] по изучению обтекания двумерного квадратного препятствия под нулевым углом скольжения на основе картин визуализации было установлено, что ос-редненная линия присоединения оторвавшегося потока в зоне квази-двумерного обтекания параллельна образующей цилиндрического тела (рис. 1.12, а, б). Это указывает на малую скорость существующего поперечного течения.[ ...]
На рис. 1.12 представлены фрагменты картин течения при различных углах ориентации двумерных моделей призматических тел квадратного сечения относительно вектора скорости набегающего потока, полученные методом «сажемасляной пленки». Видно, что наличие угла скольжения приводит к трансформации течения. Оно перестраивается, усиливается вторичное течение за препятствием вдоль его образующей. Анализ большого числа фотографий показал, что до угла скольжения примерно 15° линия присоединения оторвавшегося потока остается практически параллельной образующей препятствия, затем она при увеличении угла скольжения все больше отклоняется в направлении основного потока. Это можно объяснить усилением вторичного течения за счет искривления линий тока.[ ...]
Полученные данные служат основанием для предположения, что двумерный подход, основанный на классической концепции равновесного течения Таунсенда для двумерных турбулентных пограничных слоев и на вариациях классической гипотезы о длине пути перемешивания, по-видимому, может быть использован при малых углах скольжения потока (<15°). В каждом случае это требует дополнительного теоретического и экспериментального обоснования.[ ...]
Заметим, что для получения экспериментальных данных по обтеканию препятствий на плоской стенке при малых углах скольжения по сравнению со сложными прямыми измерениями напряжения трения на стенке в трехмерных потоках можно использовать более простой подход с применением косвенных диагностических устройств, не чувствительных к углам скоса потока (например, микронасадки Престона и поверхностные тепловые датчики), в сочетании с методами визуализации потока для определения его направления.[ ...]
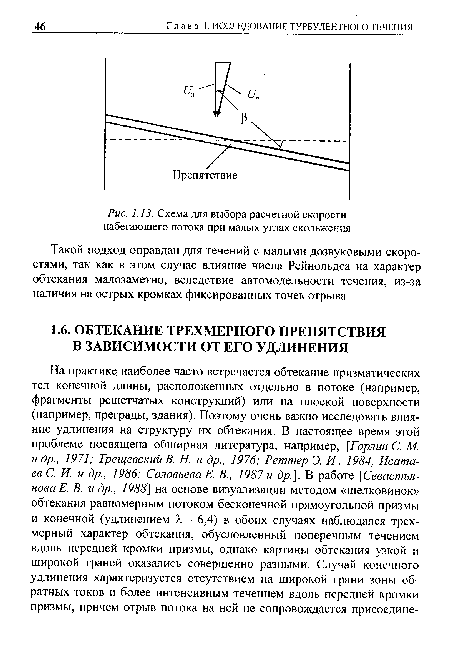
В случаях, когда отсутствуют экспериментальные данные при малых углах скольжения, в качестве первого приближения к определению положения зоны присоединения оторвавшегося потока на участках размаха, где мало влияние концевых вихрей, может быть применена та же вычислительная процедура, что и в случае Р = 0, с поправкой на величину скорости набегающего потока, т. е. расчет следует проводить для скорости и„ = и0- соэ р (рис. 1.13).[ ...]
Глава 1. ИССЛЕДОВАНИЕ ТУРБУЛЕНТНОГО ТЕЧЕНИЯ.[ ...]
Такой подход оправдан для течений с малыми дозвуковыми скоростями, так как в этом случае влияние числа Рейнольдса на характер обтекания малозаметно, вследствие автомодельности течения, из-за наличия на острых кромках фиксированных точек отрыва.[ ...]
Рисунки к данной главе:
| Схема пристенного течения при обтекании двумерного препятствия под углом скольжения |
 |
| Визуализация картин обтекания двумерного препятствия при отсутствии и наличии угла скольжения |
 |
| Схема для выбора расчетной скорости набегающего потока при малых углах скольжения |
 |