Геометрия кучевых облаков весьма причудлива, нерегулярна, недостаточно хорошо изучена и очень трудно поддается аналитическому описанию. По этой причине специалисты, занимающиеся моделированием переноса излучения, вынуждены использовать, по крайней мере на первом этапе исследований, аппроксимации конфигурации реальных облаков простейшими геометрическими телами: сферами, опрокинутыми усеченными параболоидами вращения, цилиндрами и т.д. Такая неоднозначность в моделировании конфигурации облаков стимулировала проведение специальных исследований [22, 25-27, 29] с целью оценки чувствительности средних лучистых потоков к вариациям геометрической формы облаков.[ ...]
В какой-то степени ответить на эти вопросы позволяют результаты, представленные в работе [30], где используется модель кучевых облаков, генерируемая пуассоновским потоком точек в пространстве. Облака аппроксимировались опрокинутыми усеченными параболоидами вращения, высота которых Н равна диаметру й.[ ...]
При решении трехмерного уравнения переноса использовались периодические граничные условия, которые предполагают, что слой 0< г < АН заполнен данной реализацией облачного поля. Лучистые потоки рассчитаны методом Монте-Карло с моделированием ста миллионов траекторий, что обеспечивает относительную погрешность вычислений, не превышающую 2%. Пропускание определено на нижней (плоскость 2 = 0), а альбедо - на верхней границе облаков (плоскость г = АН).[ ...]
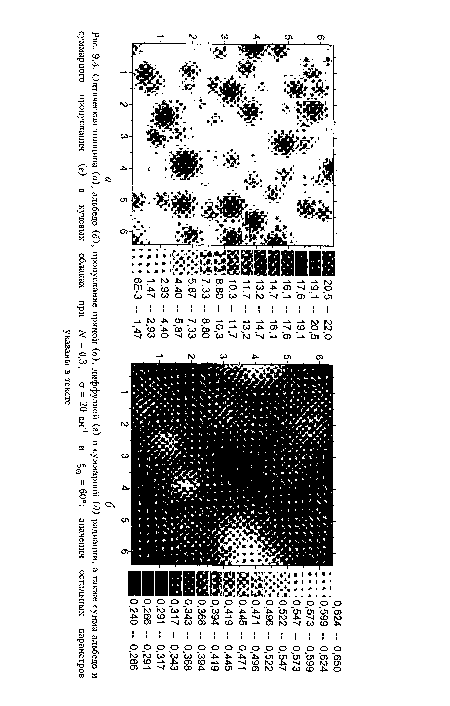
Многократное рассеяние играет существенную роль в формировании радиационного поля в облаках, поэтому альбедо Л и пропускание диффузной радиации (достигают больших значений даже в тех пикселях, которые расположены вне облаков (рис. 9.4, б, г). Облака имеют различную толщину, которая в данной реализации облачного поля изменяется от 0,033 до 1,174 км. Поле излучения, отраженное отдельным облаком, расплывается в пространстве и перекрывается с радиационными полями других облаков прежде, чем оно достигнет плоскости г- АН, где определяется альбедо. Эффекты расплывания и перекрывания настолько сильно сглаживают зависимость альбедо от горизонтальных координат, что многие детали маскируются и по известным значениям альбедо трудно визуально восстановить реальную картину распределения облаков в пространстве (рис. 9.4, а, б). Вершины наиболее мощных облаков хорошо видны, поскольку в этом случае влияние указанных выше эффектов не является достаточно сильным. Альбедо изменяется в интервале от 0,24 до 0,65, а его среднее значение равно 0,33.[ ...]
Пропускание диффузной радиации < >3 имеет наибольшие значения в пикселях с незначительной (около 2-3) оптической толщиной. Пиксели не экранируются окружающими облаками, т.е. падающая солнечная радиация достигает пикселя без взаимодействия с ними (рис. 9.4, г). Интересной особенностью является то, что в таких пикселях значения ()8 могут заметно превосходить 1. Это объясняется тем, что дополнительный вклад в пропускание диффузной радиации этими пикселями дает излучение, которое падает на соседние оптически более плотные пиксели и после многократного рассеяния "скатывается" в оптически тонкие ячейки и проходит через них. Естественно, что существуют пиксели, где значения малы (0,1-0,2), и они либо удалены от облаков на большое расстояние, либо расположены в тени наиболее мощных из них. Пропускание диффузной радиации может изменяться больше, чем на рюрядок (от 0,12 до 1,45), и его среднее значение равно 0,42.[ ...]
На рис. 9.4, д представлено пропускание суммарной радиации 5=5 + Р5, которое изменяется от 0,12 до 1,65 и имеет среднее значение 0,67. Своих наименьших значений () достигает в тех пик-целях, которые расположены в тени наиболее мощных облаков. В пикселях, расположенных в просветах между облаками, 5 = 1 и из-за дополнительного вклада диффузной радиации всегда справедливо неравенство О > 1. Очевидно, что последнее неравенство будет выполняться в тех пикселях, где ()3 > 1.[ ...]
Рисунки к данной главе:
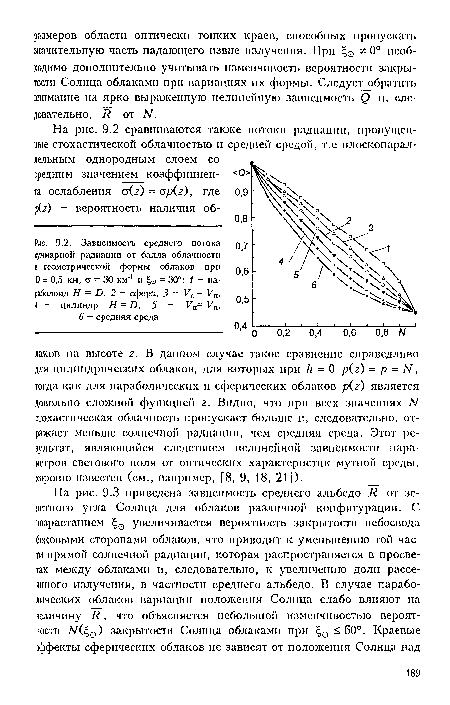
| Зависимость среднего потока д J суммарной радиации от балла облачности и геометрической формы облаков при д 0 й = 0,5 км, а - 30 км1 и = 30° |
 |
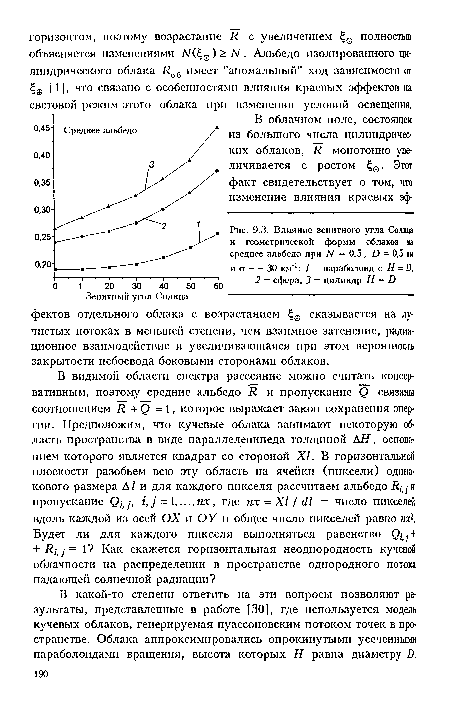
| Влияние зенитного угла Солнца и геометрической формы облаков на среднее альбедо при N = 0,5, И = 0,5 км и о = = 30 км 1 |
 |
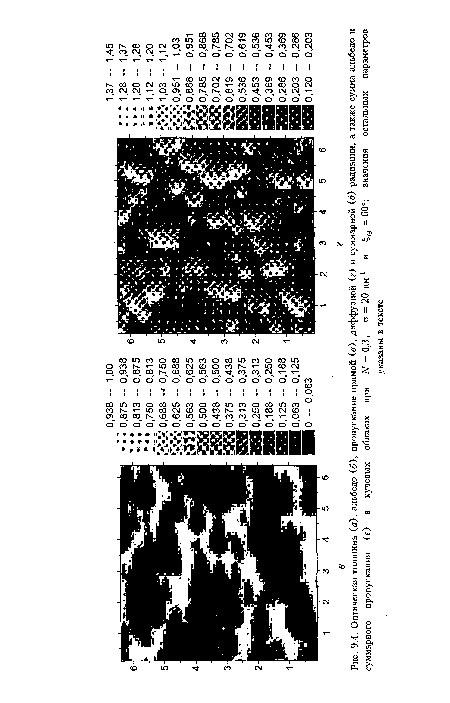
| Оптическая толщина (а), альбедо (б), пропускание прямой (в), диффузной (г) и суммарной (Э) суммарного пропускания (е) в кучевых облаках при N = 0,3, а = 20 км 1 и §© = 60°; |
 |