Входными параметрами радиационных блоков как составной части всех существующих моделей климата являются оптические характеристики: индикатриса рассеяния, коэффициент ослабления и альбедо однократного рассеяния, известные для всех длин волн. Поскольку капли воды имеют почти сферическую форму, то для жидкокапельных облаков эти характеристики рассчитываются по формулам теории Ми. Спектр размеров капель воды в среднем хорошо аппроксимируется гамма-распределением [3, 4], хотя нередки случаи, когда локальные спектры имеют бимодальный вид и неудовлетворительно описываются этим распределением [7]. В расчетах потоков и полей яркости облаков обычно используются оптические характеристики, вычисленные при максимальном радиусе капель гтах 20 -г- 30 мкм [3]. Выбор такого значения гтах основывается до сих пор на широко распространенном мнении, что радиационные поля в облачной атмосфере якобы слабо зависят от распределения капель по размерам (см., например, [42]), поэтому влиянием больших капель можно пренебречь. Немаловажную роль играет и то обстоятельство, что при больших радиусах капель г соответствующие ряды сходятся очень медленно и требуются большие затраты компьютерного времени. Однако эта аргументация явно неубедительна, поскольку основывается на расчетах переноса излучения с оптическими характеристиками облаков, которые были предварительно вычислены при ггпах 20 30 мкм.[ ...]
Эффект больших капель. Натурные измерения показывают (см., например, [7, 9, 27, 28], что большие капли (радиус > 40 т 50 мкм) присутствуют, как правило, даже в тех облаках, которые еще не содержат осадки. С увеличением размера концентрация крупных капель убывает заметно медленнее, чем по экспоненте, и при г > 100 мкм сглаживается степенной зависимостью [7].[ ...]
С учетом крупных капель оптические характеристики облаков меняются следующим образом [4]: 1) эффективный размер частиц ге увеличивается, и согласно соотношению (5.4) при фиксированном водозапасе оптическая толщина уменьшается; 2) индикатриса рассеяния становится более вытянутой вперед, т.е. фактор асимметрии возрастает; 3) альбедо однократного рассеяния уменьшается. Такие изменения оптических параметров приводят к уменьшению альбедо, а также к пзмеиешно других радиационных характеристик облаков.[ ...]
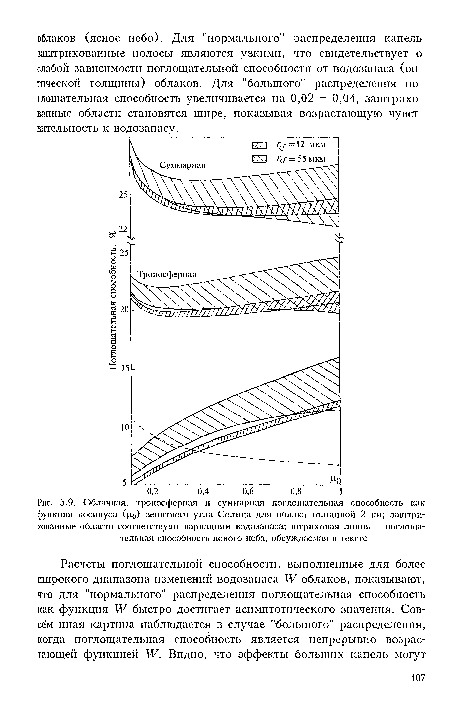
Спектральное альбедо на верхней границе облаков представ леио на рис. 5.10 [51]. Сильные полосы водяного пара с центрами примерно 0,95; 1,1; 1,4 п 1,9 мкм обусловливают глубокие минимумы. Для "нормального" распределения капель видимое альбедо облаков около 0,9, и это значение выше наблюдаемых, которые редко превосходят 0,85. Это различие можно объяснить тем, что расчеты основаны на модели, не учитывающей неоднородность облаков, и выполнены для больших значений водозапаса. Однако необходимо рассматривать и другой фактор: большие капли могут эффективно (на 10 -20%) уменьшать альбедо облаков и планеты в целом.[ ...]
Следует также отметить, что присутствие больших капель может играть важную роль в перераспределении нагревания за счет поглощения солнечной радиации в облаках и, в частности, изменять их парниковый эффект.[ ...]
В работе [40] высказывается предположение, что обратное рассеяние на маленьких иесферпческнх ледяных кристаллах является ответственным за высокие значения альбедо, измеренные над полями перистых облаков.[ ...]
Рисунки к данной главе:
| Нормированные на единичную концентрацию распределения капель (а) и водности (б) по размерам |
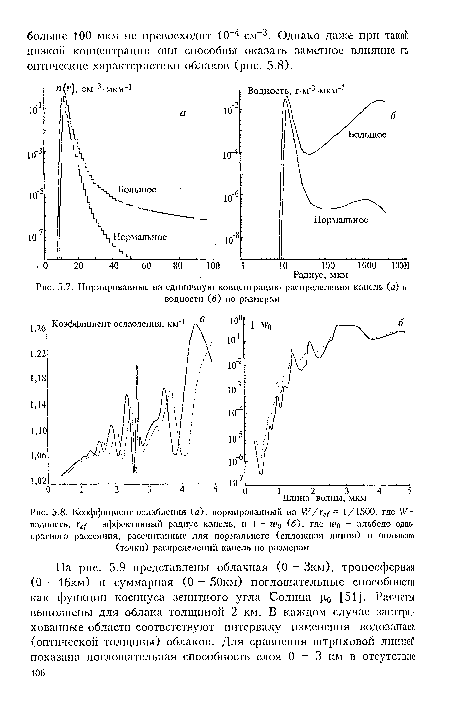 |
| Коэффициент ослабления (а), нормированный на 1¥/г^= 1/1500. где W’-водность, ге{ - эффективный радиус капель, и 1 - т§ (б), где Шо |
 |
| Спектральное альбедо как функция длины волны |
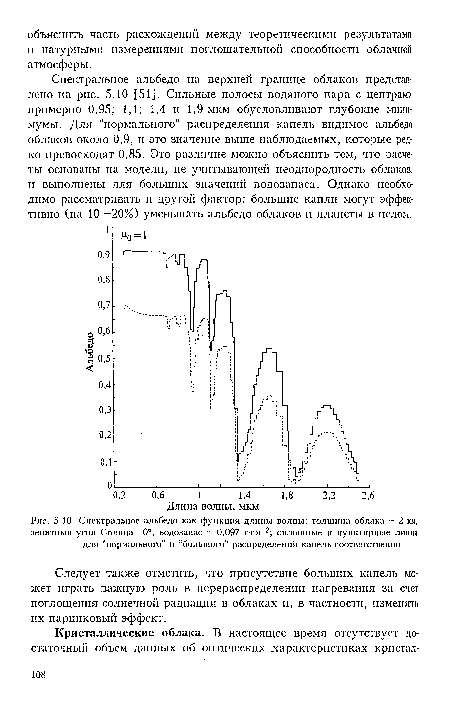 |
| Размеры, форма и концентрация кристаллов льда в перистых облаках |
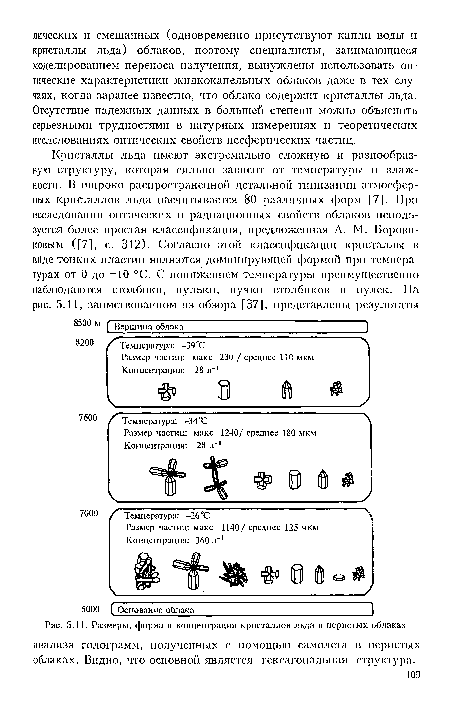 |
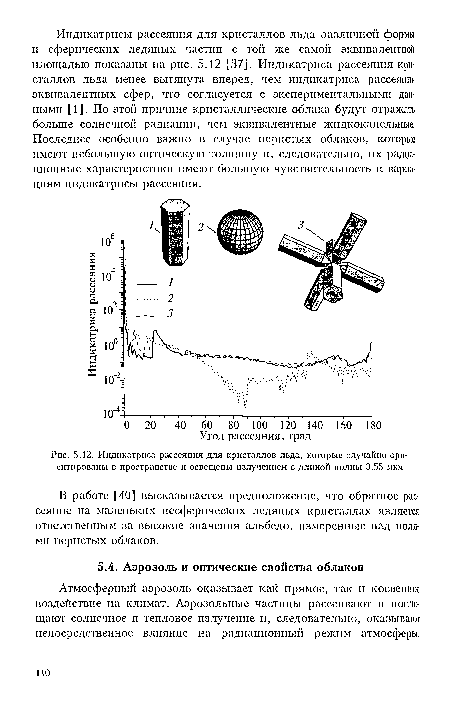
| Индикатриса рассеяния для кристаллов льда, которые случайно ориентированы в пространстве н освещены излучением с длиной волны 0,55 мкм |
 |