Моделирование - метод исследования объекта (явления, процесса, устройства) на модели - давно используется в различных областях науки и техники. Суть его состоит в том, что исследование самого объекта заменяют исследованием его модели. Полученные свойства модели переносят на свойства моделируемого объекта.[ ...]
Модель - специально созданный объект любой природы, более простой по сравнению с исследуемым по всем свойствам, кроме тех, которые надо изучить, и способный заменить исследуемый объект так, чтобы можно было получить новую информацию о нем.[ ...]
Известный пример моделирования: обтекание самолета, летящего в воздухе, исследуют обтеканием его модели в аэродинамической трубе. В данном случае модель самолета - его геометрически подобная уменьшенная копия. Моделируется (исследуется) только обтекание корпуса самолета потоком воздуха и не исследуются другие свойства самолета, например удобство и безопасность пассажира в кресле. Для этого надо построить другую модель - отдельное кресло с манекеном на устройстве, воспроизводящем возможные его положения в полете. Как видим, модель учитывает какие-то явления (обтекание корпуса самолета потоком воздуха в одном случае или расположение человека в кресле в другом случае при моделировании разных процессов в самолете) и параметры процессов (конфигурация крыльев и корпуса или конфигурация кресла). Учитываемые в модели явления назовем составляющими модели.[ ...]
Некоторые комментарии к определению модели. Ее специально создают, чтобы исследовать какие-либо конкретные свойства. Для изучения разных свойств объекта может быть создано несколько его моделей, каждая из которых отвечает определенной цели исследования. Можно говорить о единстве “цель -модель”. Если модель отражает большее (или меньшее) число свойств, то она называется более широкой (или более узкой). Используемое иногда понятие “общая модель” как модель, отражающая все свойства объекта, - бессмысленно по сути.[ ...]
Обратим внимание на следующий признак модели: она должна предсказывать неизвестные свойства объекта, давать о нем новую информацию. Это может быть достигнуто, во-первых, если модель простая, и ее можно исследовать, работать с ней, и, во-вторых, если она достаточно полная, чтобы могли проявиться изучаемые свойства.[ ...]
Трудности масштабного перехода для реакционных процессов удается преодолеть, используя математическое моделирование, в котором модель и объект имеют разную физическую природу, но одинаковые свойства. Два устройства - механический маятник и замкнутый электрический контур, состоящий из конденсатора и катушки индуктивности, - имеют разную физическую природу, но одинаковое свойство: колебания механические и электрические соответственно. Можно так подобрать параметры этих устройств (длину маятника и отношение емкости к индуктивности), что колебания по частоте будут одинаковыми. Тогда электрический колебательный контур будет моделью маятника. Это возможно потому, что свойство обоих устройств - колебания - описывается одними и теми же уравнениями. Отсюда и название вида моделирования - математическое. Уравнение колебания в данном случае также является математической моделью и механического маятника, и электрического контура. Соответственно, математические модели подразделяются на реальные, представленные неким физическим устройством, и знаковые, представленные математическими уравнениями. Классификация моделей приведена на рис. 2.4.[ ...]
Естественно, для построения реальной математической модели надо сначала создать знаковую. Поэтому, как правило, математическую модель отождествляют только с уравнениями, описывающими объект, т. е. со знаковой математической моделью, а исследование свойств этих уравнений называют математическим моделированием. Универсальной реальной математической моделью является электронная вычислительная машина (ЭВМ). По уравнениям, описывающим объект, ЭВМ “настраивают” (программируют), и ее “поведение” будет описываться этими уравнениями.[ ...]
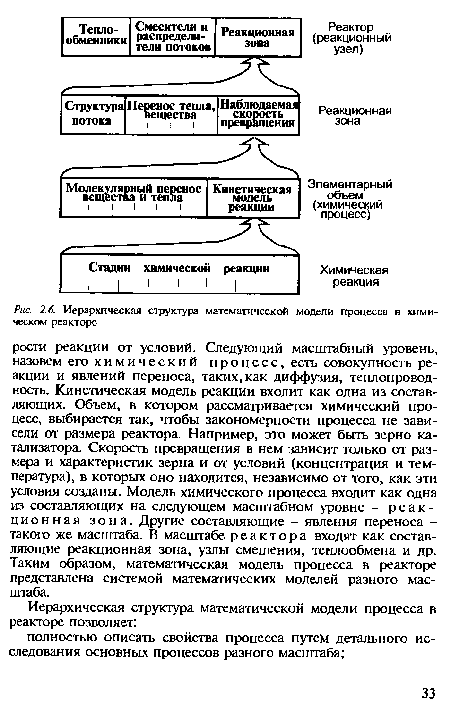
Выделение составляющих сложного процесса (его декомпозиция) должно отвечать также условию инвариантности выделенных составляющих к масштабу, влияние которого учитывают в параметрах полученных уравнений математической модели и граничных условиях. Требование инвариантности можно удовлетворить, если использовать иерархический подход к построению модели. Для этого декомпозицию процесса проводят не только на составляющие, но и по их масштабу. Существенной особенностью математических моделей процесса в реакторах является их иерархическое строение (рис. 2.6).[ ...]
Изучение процесса в химическом реакторе будем проводить описанным выше научным методом - математическим моделированием.[ ...]
Рисунки к данной главе:
| Классификация моделей |
 |
| Иерархическая структура математической модели процесса в химическом реакторе |
 |