Случайной величиной называется величина, которая в результате испытаний может принимать одно из возможных заранее неизвестных значений. В теории надежности оперируют с такими случайными величинами, как ресурс, наработка до отказа, число отказов за некоторый период эксплуатации, время восстановления и др. Случайные величины могут быть непрерывного или дискретного типа.[ ...]
Случайная величина называется непрерывной, если она может в результате испытаний принять любое значение в одном или нескольких заданных интервалах.[ ...]
Случайная величина называется дискретной, если она может принимать конечное или бесконечное счетное множество значений, то есть если эти значения могут быть пронумерованы в каком-нибудь порядке. К дискретным случайным величинам относятся данные статистических (эмпирических) наблюдений об отказах объектов — наработка до отказа, число отказов и др.[ ...]
Для полной характеристики случайной величины необходимо задать не только все возможные ее значения, но и закон ее распределения.[ ...]
Законом распределения называется зависимость, устанавливающая связь между возможными значениями случайной величины и их вероятностями. При расчетах надежности установление закона распределения является необходимой процедурой для получения исходных данных для расчета показателей надежности.[ ...]
Функция F x) является неубывающей функцией х (монотонно возрастающей для непрерывных процессов и ступенчато возрастающей для дискретных процессов). В пределах изменения случайной величины X она изменяется от 0 до 1.[ ...]
Она характеризует частость повторений данного значения случайной величины t. В задачах надежности она широко используется как плотность вероятности.[ ...]
В ряде случаев достаточно характеризовать распределение случайной величины некоторыми числовыми величинами: математическим ожиданием (средним значением); модой и медианой, характеризующими положение центров группирования случайных величин по оси абсцисс; дисперсией, средним квадратическим отклонением, коэффициентом вариации, характеризующими рассеивание случайной величины.[ ...]
При достаточно большом числе испытаний (наблюдений) полагают, что Mt = Т.[ ...]
Квантилем называется значение случайной величины, соответствующее заданной вероятности.[ ...]
Рисунки к данной главе:
| Экспоненциальный закон распределения наработки |
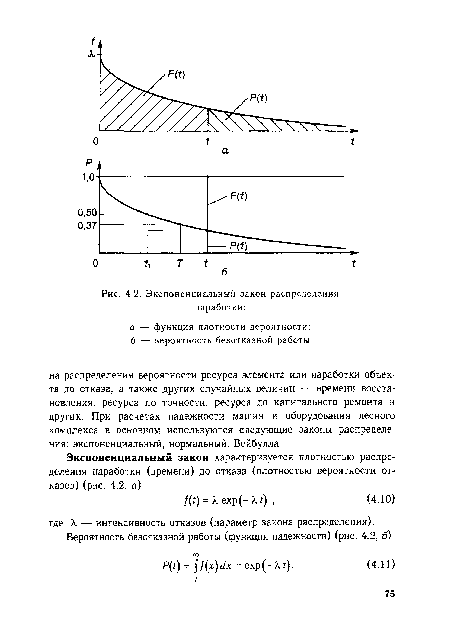 |
| Распределение Вейбулла |
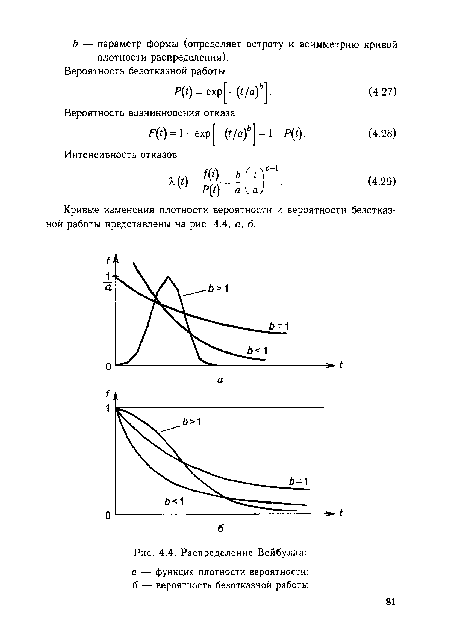 |