Для практических задач очистки сточных вод от нефтепродукта большой интерес представляет механика жидких частиц, т. е. движение жидких капель в жидкой среде.[ ...]
Движение жидкой капли в жидкой среде существенно отличается от движения жесткой сферы в аналогичных условиях и является значительно более сложным. Первое отличие состоит именно в том, что жидкая капля не является жесткой и в процессе движения может изменять форму. Это явление очень хорошо на-блюдается при движении воздушного пузыря в жидкой среде. На пузырь воздуха действуют подъемная сила, а также силы сопротивления жидкости и поверхностного натяжения. Последняя сила стремится придать пузырю шарообразную форму. В то же время сила сопротивления создает неравномерное по окружности давление на шар. В результате действия этой силы шарообразная форма нарушается. Чем меньше пузырьки газа, тем больше силы поверхностного натяжения и тем устойчивее его форма. Весьма небольшие пузыри почти всегда были шарообразными. У больших пузырей влияние поверхностного натяжения по сравнению с динамическим воздействием жидкости меньше, и шар сплющивается, приобретая различные неустойчивые формы. Такая форма тела приводит к колебаниям скорости его всплытия и к отклонениям траектории движения от вертикали. Возникает осцилляция (колебательное изменение формы) капель, как это схематически показано на рис. 4.5. Для характеристики размеров капель вводится понятие эквивалентного диаметра (диаметра сферы, имеющего объем, равный объему капли).[ ...]
При движении жидкой капли в жидкости специфическим образом проявляются физические свойства системы, в частности, вязкость жидкости капли и среды, в которой она движется, а также поверхностное натяжение на границе раздела фаз.[ ...]
Существенно различаются явления в поверхностных слоях жидкости, обтекающей жидкую каплю и жесткую сферу, а также условия скольжения жидкости. При некоторых условиях в капле возникает внутренняя циркуляция жидкости, как это показано на рис. 4.6.[ ...]
При /С=1 формула Адамара—Рыбчинского превращается в формулу Стокса для жесткой сферы в потоке вязкой жидкости.[ ...]
Если е = 0, формула превращается в формулу Адамара—Рыбчинского.[ ...]
При очень малых размерах капель, если принять г = О, формула превращается в формулу Стокса.[ ...]
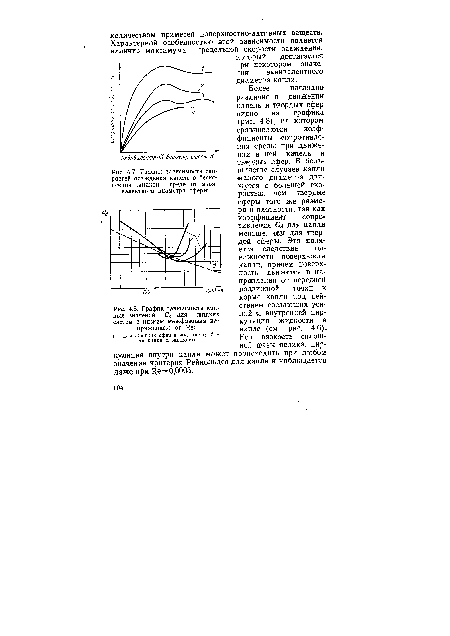
Более наглядно различие в движении капель и твердых сфер видно из графика (рис. 4.8), на котором сравниваются коэффициенты сопротивления среды при движении в ней капель и твердых сфер. В большинстве случаев капли малого диаметра движутся с большей скоростью, чем твердые сферы того же размера и шлотности, так как коэффициент сопротивления Са для капли меньше, чем для твердой сферы. Это является следствие подвижности поверхности капли, причем поверхность движется в направлении от передней подвижной точки к корме капли под действием срезающих усилий и внутренней циркуляции жидкости в капле (см. рис. 4.6). Если вязкость сплошной фазы велика, циркуляция внутри капли может происходить при любом значении критерия Рейнольдса для капли и наблюдается даже при Яе=0,0003.[ ...]
Капли периодически осциллируют, принимая последовательно шарообразную и эллипсоидальную форму. Форма очень крупных капель становится неопределенной, осцилляция их совершенно беспорядочна. Форма и осцилляция капель в конечном счете влияют на скорость осаждения, которая достигает максимума или проходит через максимум (см. рис. 4.7). Соответственно увеличивается и коэффициент трения, который с некоторого значения начинает превышать коэффициент трения для твердой частицы. Величина максимума зависит от физических свойств жидкости.[ ...]
Все приведенные рассуждения относились к движению одиночной сферы в полубесконечном пространстве. В действительности в сточных водах движение одиночной частицы происходит при наличии бесконечного числа однородных и неоднородных частиц разных размеров. Если для частицы очень маленьких размеров ее движение подчиняется закону Стокса, то для частицы больших диаметров этот закон будет нарушен. Как было показано на рис. 4.5, движение капли средних размеров происходит не по прямой линии, а по какой-то ломаной. При наличии в жидкости частиц больших размеров, двигающихся с большой скоростью, при определенных числах Рейнольдса происходит частичный срыв пограничного слоя с поверхности частицы. Это приводит к резкому ухудшению условий обтекания тела частицы. Благодаря срыву ламинарного слоя изменяется распределение давления по поверхности тела. В результате, этого происходит деформация жидких частиц, если силы воздействия оказываются больше силы поверхностного натяжения, которая стремится придать жидкой частице форму шара.[ ...]
Рисунки к данной главе:
| Теоретический (сплошная линия) и практический (пунктирная линия) характер движения одиночного пузыря. Примечание. Буквами обозначены скорости движения пузыря |
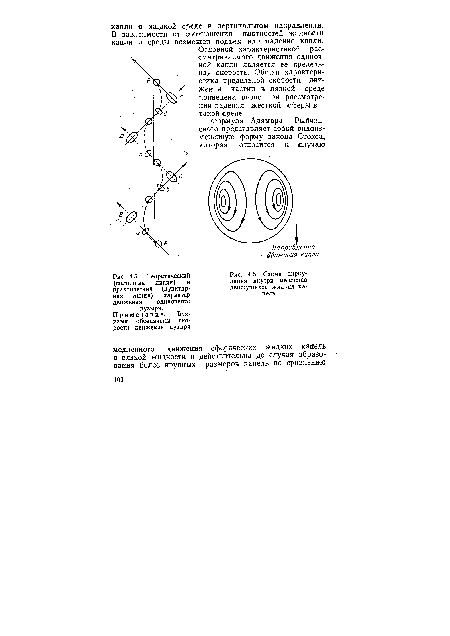 |
| Схема циркуляции внутри медленно движущихся жидких капель |
 |
| График зависимости кривых значений С& для жидких систем с низким межфазовым напряжением от Ие |
 |
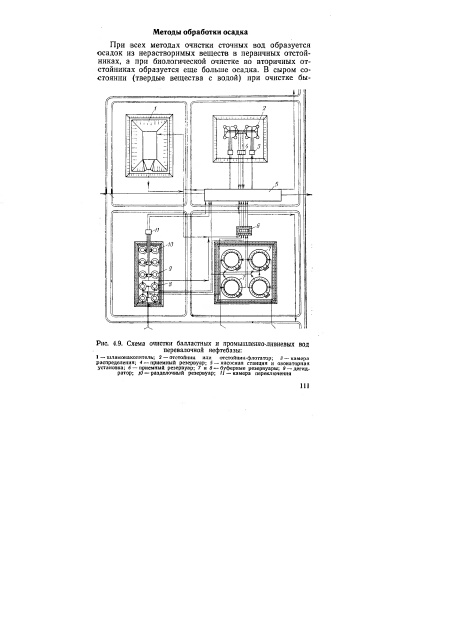
| Схема очистки балластных и промышленно-ливневых вод перевалочной нефтебазы |
 |
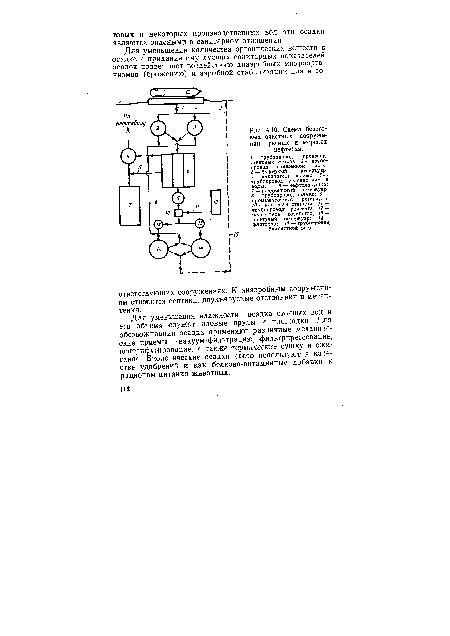
| Схема береговых очистных сооружений речных и морских нефтебаз |
 |