Первые работы в этой области принадлежат И. Ньютону.[ ...]
Основным, в определенной степени переломным, моментом развития теории в рассматриваемой области является классическая работа Д. Г. Стокса об обтекании шара, которая в значительной степени была подготовлена предшествующими исследованиями в области гидравлики и гидродинамики.[ ...]
Эта работа положила начало проблеме, которая получила название задачи Стокса.[ ...]
Задача Стокса имеет большое значение в некоторых принципиальных задачах теоретической физики и термодинамики. Разработка этой проблемы прошла ряд этапов и продолжается в настоящее время.[ ...]
Метод расчета очистных сооружений во многих случаях базируется на теоретических основах гидромеханики. В механике жидкостей сложился самостоятельный раздел, в котором рассматривается механика частиц дисперсной фазы в потоке и неподвижной жидкости.[ ...]
Частицы дисперсной фазы в жидкой дисперсной среде могут быть в твердом, жидком и газообразном состояниях и иметь различные размеры и форму. Более подробно определена механика частиц сферической формы, хотя разрабатываются некоторые задачи механики и при другой форме частиц.[ ...]
В зависимости от агрегатного состояния частиц рассматривается механика: твердых частиц и жидких капель в вязкой среде; газовых, в частности, воздушных пузырьков в вязкой среде.[ ...]
Механика частиц в вязкой среде имеет ряд общих положений, справедливых независимо от агрегатного состояния частиц. Кроме того, механика частиц, различных по агрегатному состоянию, имеет существенные особенности, в отличие от механики твердых сред в жидкости.[ ...]
Последний случай представляет большой практический интерес для очистки стоков, содержащих нефтепродукты. При этом происходит взаимодействие и коалесценция (слияние) частиц, что приводит к увеличению их размера. Это является одним из основных факторов, влияющих на скорость движения частиц в жидкости.[ ...]
В механике жидкостей рассматривается также задача о медленном движении твердой сферы (шара) в жидкости. Эта задача принимается идентично задаче о медленном обтекании шара жидкостью. Для большого числа практических задач такое отождествление является допустимым. Однако в некоторых случаях рассматриваемые задачи не считаются строго идентичными.[ ...]
Рисунки к данной главе:
| Схема сил, действующих на сферу в спокойной жидкости |
 |
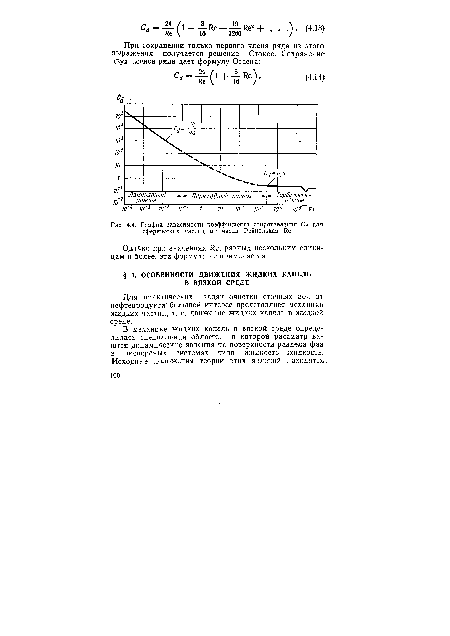
| График зависимости коэффициента сопротивления Сл для сферических частиц от числа Рейнольдса Ие |
 |