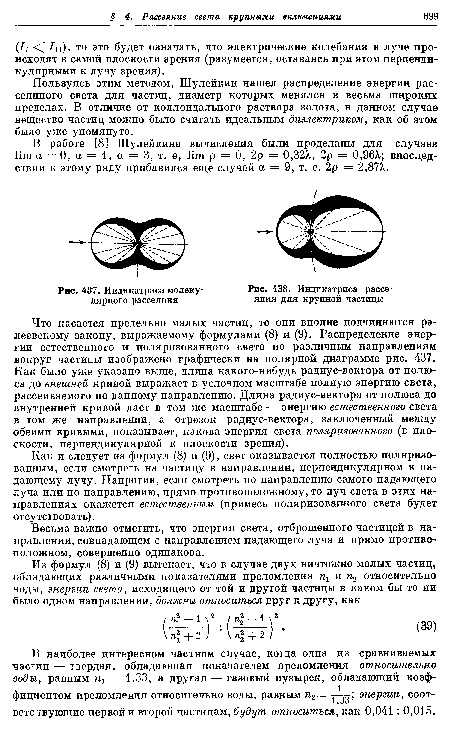
Несколько дальше, на рис. 437, графически представлено распределение радиации вокруг излучающей частицы. Внешняя кривая полярной диаграммы выражает полную энергию света, рассеиваемого частицей по всем направлениям. Радиус-вектор, проведенный к этой кривой из полюса (совпадающего с центром частицы) по какому-либо направлению, выражает в условном масштабе энергию, рассеянную в этом направлении. Внутренняя кривая проведена для нахождения поляризации света в различных направлениях: отрезок радиус-вектора, заключенный между обеими кривыми, дает энергию поляризованного света. Как было уже сказано, поляризация оказывается полной по направлениям, перпендикулярным к падающему лучу (направление падающего луча изображено стрелкой).~~В сущности полярную диаграмму, изображенную на рис. 437, следует рассматривать как пространственную; картина рассеяния будет совершенно симметрична относительно большой оси кривой, совпадающей по направлению с падающим лучом, а потому достаточно представить себе поверхность вращения, описанную обеими кривыми при вращении их вокруг большой оси,— эта поверхность вращения позволит найти энергию рассеянного света в любом направлении в пространстве.~~Что касается предельно малых частиц, то они вполне подчиняются рэ-леевскому закону, выражаемому формулами (8) и (9). Распределение энергии естественного и поляризованного света по различным направлениям вокруг частицы изображено графически на полярной диаграмме рис. 437. Как было уже указано выше, длина какого-нибудь радиус-вектора от полюса до внешней кривой выражает в условном масштабе полную энергию света, рассеиваемого по данному направлению. Длина радиус-вектора от полюса до внутренней кривой дает в том же масштабе — энергию естественного света в том же направлении, а отрезок радиус-вектора, заключенный между обеими кривыми, показывает, какова энергия света поляризованного (в плоскости, перпендикулярной к плоскости зрения).
Вернуться к оглавлению